Привет меня зовут Давид, а вот я собственной персоной отрендеренный своим самописным рендером:


К сожалению я не смог найти более качественную бесплатную модель, но все равно выражаю благодарность заморскому скульптору запечатлевшему меня в цифре! И как вы уже догадались, речь пойдет о написании CPU — рендера.

Математики давно пытаются привыкнуть к тому, что некоторые задачи в принципе невозможно решить

Мы любим повторять, что всё возможно. В книге Джастера Нортона «Мило и волшебная будка» король отказывается сообщить Мило, что его цель недостижима, поскольку «многое становится возможным, если не знаешь, что оно невозможно» [правда, это слова других персонажей книги / прим. перев.]. Но в реальном мире некоторые вещи и вправду невозможны, и мы можем доказать это при помощи математики.

Люди используют термин «невозможно» разными способами. Он может описывать просто маловероятные вещи – такие, как найти две одинаковых колоды перемешанных карт. Он может описывать задачи, практически невозможные по причине отсутствия времени, места или ресурсов – такие, как переписать всю Библиотеку Конгресса от руки. Устройства типа вечного двигателя невозможны физически, поскольку их существование противоречило бы нашему пониманию физики.

Вот что строил испанский архитектор Антонио Гауди:



Его здания описывают как «бионические дома», некоторые говорят о «летящей пластичной материи». За морем восторгов художников и дизайнеров, как мне показалось, упущена некоторая невероятная рационализация и прагматичность. Гауди был в первую очередь отличным разработчиком, математиком и геометром. Но чтобы объяснить это, сначала я покажу другую картинку:


Это два крепления. Первое производится серийно — оно просто в проектировании, просто в изготовлении, дёшево и невероятно уродливо. Второе красивое, и требует на 25% меньше материала для того, чтобы выдержать тот же вес (то есть — куда прочнее). Только его трудно рассчитать, оно будет дороже в серии — и придётся подумать.

Примерно то же самое делал Гауди. Ему пришлось обойтись без математического аппарата и современных материалов. И ещё действовать в рамках строго ограниченного бюджета. Он, фактически, заложил новые принципы всего от фасада до последней дверной ручки, создал шедевры оптимизации — в общем смёл все стереотипы как сухие листья, создал с нуля теорию и воплотил её. В девятнадцатом веке всё то, что он делал, было просто диким. Некоторые даже считали его сумасшедшим.

Сегодня мы поговорим об одной из первых задач теории больших сетей, которая может быть решена полностью на самом простом базовом уровне, но которая от этого не становится менее интересной. Это задача о кратчайшей системе дорог или задача Штейнера.

Впервые она появилась, когда еще никаких практических надобностей для больших сетей не было: в тридцатые годы XX века. На самом деле Штейнер начал ее изучать еще раньше, в XIX веке. Это была чисто геометрическая задача, практические приложения которой стали известны только несколько десятилетий спустя.

Разговор пойдет о той области математики, которая впоследствии выросла в теорию больших сетей и разбилась на несколько областей. Это прикладная отрасль, которая задействует очень много методов из других математических дисциплин: дискретной математики, теории графов, функционального анализа, теории чисел и т.д. Бурное развитие теории больших сетей пришлось на конец девяностых и начало двухтысячных годов. Связано это конечно, с прикладными задачами: развитием интернета, мобильной связи, транспортных задач для больших городов. Кроме того теория сетей используется в биологии (нейронные сети), при построении больших электронных плат и т.п.



Сама задача формулируется очень просто. Есть несколько точек на плоскости, которые нужно связать системой дорог наименьшей суммарной длины таким образом, чтобы по этим дорогам можно было из каждой точки добраться в любую другую. Число точек конечно.

Начать рассказ стоит с истории о том, как на Малом мехмате двум группам учеников – восьмиклассникам и одиннадцатиклассникам дали решать одну и ту же задачу. Четыре деревни расположены в вершинах квадрата со стороной четыре километра. Существует ли система дорог, которая связывала бы все эти деревни между собой и имела бы суммарную длину не превосходящую 11 километров.

Недавно перевел замечательный видеоролик. Вы знаете, что сферу в трёхмерном пространстве можно вывернуть наизнанку в классе погружений, т. е. с возможными самопересечениями, но без перегибов, а окружность нельзя?

В ролике наглядно показан способ выворачивания сферы, изобретенный не так давно Уильямом Терстеном. Сначала это кажется чем-то невероятно сложным и просто немыслимым, однако к концу ролика все становится понятно. Посмотрите до конца, и вы не пожалеете!:)

Для студентов технических специальностей ВУЗов в качестве исторической справки.
Заведующая автомобильно-механическим отделением Лозовского филиала Харьковского автомобильно-дорожного техникума, преподаватель высшей категории, Кожокару Елена Владимировна

125 лет назад, 31 марта 1889 г., состоялось официальное открытие самой узнаваемой архитектурной достопримечательности Парижа — Эйфелевой башни. Теперь она известна во всем мире как символ Франции.

Во время строительства Густав Эйфель решил выгравировать под первым балконом башни, на всех четырёх её сторонах, имена 72-х самых известных французских инженеров, математиков и ученых, которые внесли весомый вклад в историю развития науки. Причем, какой-либо алфавитный или хронологический порядок следования имён на башне отсутствует.


Эйфелева башня, Париж

Всем привет! Когда-то давным-давно я делал простенькие игрушки на Flash. Например: игрушка — провести курсор мышки через лабиринт, не касаясь стен и уворачиваясь от всяких движущихся объектов. Некоторые из этих объектов двигаются по заданной траектории, некоторые гонятся за курсором, а некоторые стреляют в курсор другими движущимися объектами.

Сейчас я увлёкся программированием под андроид и сделал примерно такую же игрушку. И столкнулся с теми же геометрическими задачками с которыми встречался тогда.

Более 50 лет назад автор популярных статей о математике в журнале Scientific American Мартин Гарднер предложил читателям задачу: «Можете ли вы разместить семь сигарет таким образом, чтобы каждая из них соприкасалась со всеми остальными?»

Облачные решения хороши тем, что позволяют создавать проекты любой сложности, вплоть до виртуального дата-центра. Если попробовать визуализировать эти структуры, то получится этакая мини-вселенная. Давайте поиграем с геометрией, попробовав визуализировать разные модели нашей вселенной.

В нашем сознании вселенная кажется бесконечной. Но с помощью геометрии мы можем рассмотреть различные трехмерные формы, которые предлагают альтернативу «обычному» бесконечному пространству.

Привет, Хабр! Сегодня мы очень подробно расскажем о неочевидных моментах в такой, казалось бы, простой операции: исправлении проективных искажений на изображении. Как это часто оказывается в жизни, нам пришлось выбирать, что важнее: качество или скорость. И чтобы достичь некого баланса мы вспомнили об алгоритмах, которые активно исследовали еще в 80-90-е годы в рамках задачи рендеринга структур, и с тех пор редко вспоминали в контексте обработки изображений. Если интересно, заглядывайте под кат!

Прочитав статью про семь соприкасающихся цилиндров, я задумался: действительно ли эта задача такая сложная? Или ей просто раньше никто всерьёз не занимался?
Положение бесконечного цилиндра известного радиуса в пространстве задаётся четырьмя независимыми величинами (имеет 4 степени свободы). Для семи цилиндров в общем положении потребуется 28 величин. Каждое условие «два цилиндра касаются» даёт одно ограничение, всего остаётся 7 степеней свободы. Шесть из них — перемещения пространства, последнее остаётся на саму конфигурацию. То есть, у нас должно получиться одно или несколько однопараметрических семейств конфигураций, если только не помешает топология (из-за которой решений может не оказаться вообще).
Вместо цилиндров нам удобнее работать с прямыми. Если диаметры двух цилиндров одинаковы и равны, допустим, единице, то они касаются (внешним образом) тогда и только тогда, когда расстояние между их осями равно единице. Учтём этот факт, и пойдём искать семь красных перпендикулярных прямых...

Разливающийся Нил каждый год затапливает свои берега, а потом обнажает их вновь, оставляя открытой плодороднейшую почву. Каждый год древние египтяне должны были заново измерять свои участки земли и определять их границы. Позже, древние греки описали этот процесс и назвали его геометрией — измерением земли. Геометрия представлялась принципом установления порядка и закона в мире. Бытовая процедура стала наукой.

Древние геометры стремились найти универсальные принципы и законы, которые воплощаются в фигурах всех вещей на земле. Сегодня их открытия часто используются в дизайне. Например, типографские сетки можно строить на основе известных пропорций. Результат будет выглядеть гармонично и приятно для глаза.




Но знаем ли мы почему возникли именно такие пропорции? Какой смысл в них закрыт? Что видели древние и почему упорно применяли их для создания произведений искусства, особенно, носивших религиозный смысл?



На этом изображении XVI в. геометрия представлена женщиной. Она предается размышлениям о законах и принципах устройства мира. Мужчины, изображенные вокруг нее, воплощают эти принципы в ежедневном быту. Таким образом идеи и философские концепции находят выражение в материальных объектах и практиках.

Все мы в дизайне сегодня увлеченно занимаемся практиками, производим продукты. Однако интересно и полезно иногда вернуться к классическому образованию и даже покопать еще глубже, чтобы узнать об идеях, стоящих за нашей практикой, существующих многие сотни лет. Ну то есть больше узнать про женщину :)

Под катом я еще немного ее обрисую.

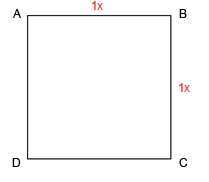
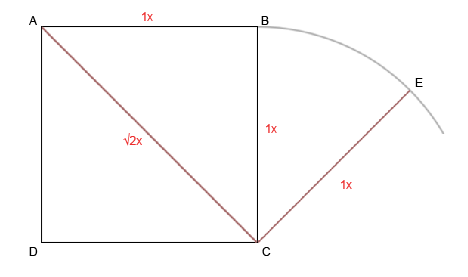
О, Боже, четвертая часть! Это выше моих сил! Спокойствие, у меня заканчиваются таблетки, поэтому это последняя статья, и в ней будут разоблачения. Под катом описание процесса подгонки, ушепритягивания, запутывания и манипуляций.

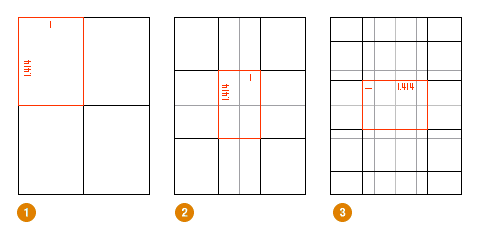
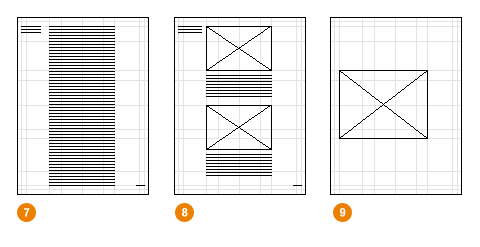
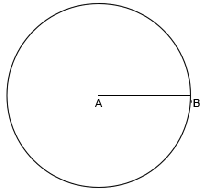
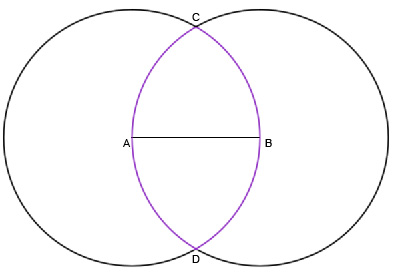
В предыдущих (1, 2, 3) частях мы видели как разные пропорции использовались в геометрии, античном искусстве и современном промышленном дизайне. У нас осталась нераскрытой тема золотого сечения и еще одного корня — √5. Начнем же.

Однажды, люди натолкнулись на идею пропорций. В различных фигурах постоянно встречались одни и те же закономерности. Это впечатляло. Потом кто-то додумался измерить парочку растений, зверюшек и некоторые части тела, которые обычно от посторонних прячут. Закономерности оказались и там. Это впечатляло еще больше.

Терпеть не осталось больше мочи, самые распространенные отношения были объявлены священными. Некоторые видели в них проявление божественного вмешательства. Некоторые — самого бога. А раз священные пропорции так часто встречаются, то можно под них подогнать все что хочешь, сделать из этого символ и стращать паству.

Мистификации и приписки из самых благих намерений встречаются в истории постоянно. Например, переписчики классического труда «Церковная история народа Англов» Беды Достопочтенного приделывали к тексту куски, дабы определенные церковные вопросы выглядели более благоприятно. А 25-28 главы VI книги «Записок о галльской войне» Цезаря по всей видимости не такие уж и Цезаря.

Так же и в символике. Надо чтобы люди чувствовали ее глубинный смысл, а сама форма не так важна. Возьми любую картинку, в ней обязательно да что-нибудь отыщется. Чем древнее, тем лучше. Самый древний у нас Египет, поупражняемся на нем.

Вот схема барельефа из гробницы Петосириса, найденной в 1919 году.



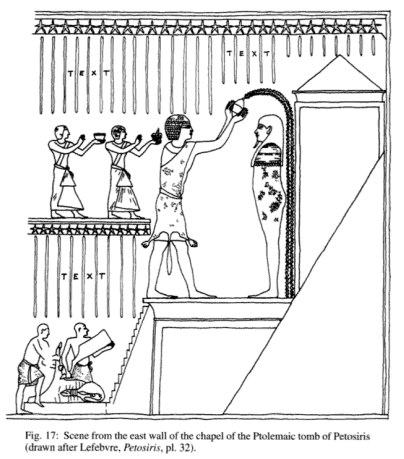
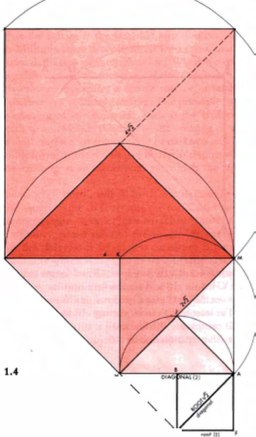
Посидев достаточное время с линейкой и циркулем, в нем можно отыскать и золотое сечение и еще кучу разных отношений (помимо буковок text, остряки, для этого не нужен циркуль).



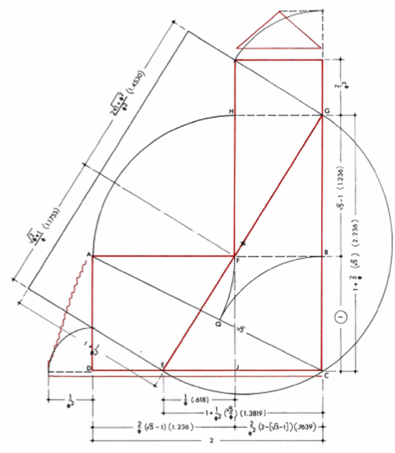
Выглядит достаточно круто, поэтому нет причин не заявить, что Египтяне знали о золотом сечении и специально все так сделали.

Мистифицировать геометрию легко и просто. Сейчас я покажу вам пару приемов. Загляните под кат.

Сейчас я вам что покажу, закачаетесь. Обязательно загляните под кат, самые интересные картинки я припрятал там.

Я продолжаю рассказ о применении философской геометрии на практике. Прошлая часть была обзорная, она говорила о том, что многие века геометрия использовалась для поиска универсальных идеальных законов природы. Эти законы повсеместно использовались в произведениях искусства, архитектуре и духовной жизни.

Сегодня я расскажу про замечательную пропорцию «корень из трех». Я покажу ее сакральный смысл, а под катом продемонстрирую пример из современного дизайна, который повергнет вас в шок ;)

Начнем с построения пропорции. Возьмем отрезок AB.



Примем его за радиус и построим окружность с центром в A.



Теперь построим вторую окружность с тем же радиусом, но с центром в B.



У нас получилась фигура ACBD, имеющая огромное значение для наших предков. Она называется Vescica Piscis (пузырь рыбы). Самый простой и важный пример — она давно является символом христианства.



Я продолжу под катом. Спорим, никогда не догадаетесь чем там все закончится :)

Еще не все копья сломались по поводу айфона, вписанного в древнюю сакральную фигуру, как у меня готово продолжение. Под катом я покажу как еще современные предметы используют идеи многовековой давности.

Эта статья — продолжение первых двух.
— Сначала был обзор, где я говорил как древние геометры искали неизменное во всем сущем и воплощали это в произведениях искусства.
— Потом была статья, где я показал как число √3 использовалось в религиозных символах и современном всем известном предмете дизайна

На этот поговорим о числе √2. Корень из двух является символом природного роста. Визуальное представление геометрической прогрессии показывает как ничтожный объект может вырасти до гигантских размеров за короткое время. Корень из двух — это то неизменное, что находится в основе этой прогрессии. В этом росте — сила данного числа.



Но что такое рост? Что вообще такое процесс творения и как ничтожное может развиваться и становиться большим? Давайте представим себе точку.



Само по себе — это ничтожество. Это сущность, присутствующая в одном измерении, но в то же время, в ней заключена огромная энергия. Давайте высвободим ее.



Что дальше? Нам нужен прорыв. Откроем для себя второе измерение. Построим квадрат ABCD



Теперь, откроем новые формы движения. С центром в точке С радиусом CB давайте проведем дугу.



Найдем новые пути движения. Соединим AC и CE. Длина AC — это √2 — фактор, удваивающий измерение.



К чему же это приведет? К бесконечному множеству вещей. Но давайте возьмем практическую задачу. Под катом мы будем выращивать идеальный ноутбук. (Можете даже не сомневаться, чей логотип там окажется :)

Английским студентам предлагается решить простую задачу по математике из вступительного экзамена в Китайский университет.

Королевское общество химии (Соединённое Королевство) выплатит приз в £500 одному счастливчику, который правильно решит задачу, взятую из китайского теста:

Вспомнилась интересная пространственная задачка с одного собеседования:

Есть 2 проекции фигуры (нет скрытых линий, т.е не шар внутри куба),
надо найти третью проекцию или нарисовать всю фигуру. Удачи.

Не оригами, но всё же. У меня не так давно произошел случай. Я что-то слушал, о чем то думал, и сгибал лист бумаги формата А4. В результате я офигел от того, что получился равносторонний треугольник. Взял линейку, обмерил — всё верно.

Хочу спросить у Вас, мои дорогие: существуют ли такие способы уже? Вряд ли я первый.

P.S. Спрашивал у интернетов — они сказали не знают.

=========================================================
UPD: В сявзи с минусующими и тем кто в поисках смысла:

Ещё раз о задаче:

Есть лист А4. Используя только сгибы сделать равносторонний треугольник.

Вопрос: кто каким путем придет к решению задачи?

Это не просто, не сложно. Это не зачем.
Я спрашиваю о последовательности действий only.