Всем привет!
Давайте поговорим о, как вы уже наверное смогли догадаться, нейронных сетях и машинном обучении. Из названия понятно, что будет рассказано о Mixture Density Networks, далее просто MDN, переводить название не хочу и оставлю как есть. Да, да, да… будет немного скучной математики и теории вероятности, но без неё, к сожалению, или к счастью, тут уж сами решайте, трудно представить мир машинного обучения. Но спешу вас успокоить, ее будет относительно мало и она будет не сильно сложная. Да и вообще ее можно будет пропустить, а просто посмотреть на небольшое количество кода на Python и PyTorch, все верно, сеть мы будем писать с помощью PyTorch, а так же на различные графики с результатами. Но самое главное то, что будет возможность немного разобраться и понять что же такое MD сети.
Что ж начнем!
Регрессия
Давайте для начала немного освежим свои знания и вспомним, совсем вкратце, что такое линейная регрессия.
У нас есть вектор
Конечно, зависимость, заложенная в природе генерации данных, может быть различная и тогда уже надо добавить в нашу модель некую нелинейность. Решать задачу регрессии напрямую для больших и реальных данных тоже плохая идея, так как там есть матрица
Но сейчас, поговорим не об этом, а о функциях ошибок. В чем разница между SE и Log-Likelihood в случае когда данные могут иметь нелинейную зависимость?
Разбираемся с зоопарком, а именно: OLS, LS, SE, MSE, RSS
Все это одно и то же по сути, RSS — residual sum of squares, OLS — ordinary least squares, LS — least squares, MSE — mean squared error, SE — squared error. В разных источниках можно встретить разные названия. Суть у этого всего одна: квадратичное отклонение. Можно запутаться конечно, но к этому быстро привыкаешь.
Стоит отметить, что MSE это среднеквадратичное отклонение, некое среднее значение ошибки для всего тренировочного набора данных. На практике обычно MSE и используется. Формула особо ничем не отличается: — размер датасета,
— размер датасета,  — предсказание модели для
— предсказание модели для  .
.
Стоит отметить, что MSE это среднеквадратичное отклонение, некое среднее значение ошибки для всего тренировочного набора данных. На практике обычно MSE и используется. Формула особо ничем не отличается:
Стоп! Likelihood? Это ведь что то из теории вероятности. Все верно — это теория вероятности в чистом виде. Но как квадратичное отклонение может быть связано с функцией правдоподобия? А как оказывается связано. Связано с нахождением максимума правдоподобия (Maximum Likelihood) и с нормальным распределением, если быть более точным, то с его средним
Для того, что бы осознать что это так, давайте еще раз посмотрим на функцию квадратичного отклонения:
Теперь, вспомнив формулу нормального распределения, получим:
Если использовать функцию среднеквадратичного отклонения MSE то из этого получим:
Вывод: Если в вопросе регрессии использовать семейство LS в качестве функций ошибки, то по сути решаем задачу нахождения максимума функции правдоподобия в случае когда распределение гауссово. А предсказанное значение
А вот и обещанный бонус. Раз уж зашла речь о связях между различными функциями ошибки, то рассмотрим (не обязательно к прочтению):
Связь между Cross-Entropy, Likelihood , Log-Likelihood и Negative Log-Likelihood
Предположим у нас есть данные  , каждая точка принадлежит определенному классу, например
, каждая точка принадлежит определенному классу, например  . Всего есть
. Всего есть  классов, при этом класс 1 встречается
классов, при этом класс 1 встречается  раз, класс 2 —
раз, класс 2 —  раз, а класс
раз, а класс  —
—  раз. На этих данных мы обучили некоторую модель
раз. На этих данных мы обучили некоторую модель  . Функция правдоподобия (Likelihood) для нее будет выглядеть так:
. Функция правдоподобия (Likelihood) для нее будет выглядеть так:
где — предсказанная вероятность для класса
— предсказанная вероятность для класса  .
.
Берем логарифм от функции правдоподобия и получаем Log-Likelihood:![$\hat{y} \in [0, 1]$](https://habrastorage.org/getpro/habr/formulas/a55/cdf/87c/a55cdf87c3da797e8284e2bcd1652b31.svg) лежит в пределах от 0 до 1, исходя из определения вероятности. Следовательно логарифм будет иметь отрицательное значение. И если умножить Log-Likelihood на -1 мы получим функцию Negative Log-Likelihood (NLL):
лежит в пределах от 0 до 1, исходя из определения вероятности. Следовательно логарифм будет иметь отрицательное значение. И если умножить Log-Likelihood на -1 мы получим функцию Negative Log-Likelihood (NLL): ,
,  , то получим:
, то получим: равна:
равна:  . Отсюда получаем:
. Отсюда получаем: то получим:
то получим: (бинарная классификация) получим формулу для binary cross entropy (так же можно встретить всем известное название Log-Loss):
(бинарная классификация) получим формулу для binary cross entropy (так же можно встретить всем известное название Log-Loss):
Пример. Рассмотрим бинарную классификацию. У нас есть значения классов:
Реальная вероятность для класса 0 равна
для класса 0 равна  , для класса 1 равна
, для класса 1 равна  . Пусть у нас есть бинарный классификатор который предсказывает вероятность класса 0
. Пусть у нас есть бинарный классификатор который предсказывает вероятность класса 0  для каждого примера, соответственно для класса 1 вероятность равна
для каждого примера, соответственно для класса 1 вероятность равна  . Построим график значений функции Log-Loss для разных предсказаний
. Построим график значений функции Log-Loss для разных предсказаний  :
:
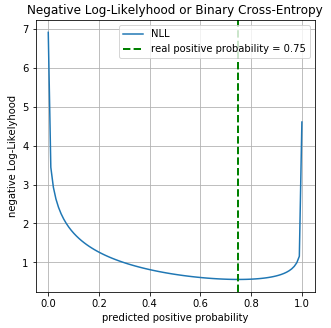
На графике можно увидеть что минимум функции Log-Loss соответствует точке 0.75, т.е. если бы наша модель полностью «выучила» распределение исходных данных, .
.
где
Берем логарифм от функции правдоподобия и получаем Log-Likelihood:
Пример. Рассмотрим бинарную классификацию. У нас есть значения классов:
y = np.array([0, 1, 1, 1, 1, 0, 1, 1]).astype(np.float32)Реальная вероятность

На графике можно увидеть что минимум функции Log-Loss соответствует точке 0.75, т.е. если бы наша модель полностью «выучила» распределение исходных данных,
Регрессия с использованием нейронных сетей
Вот мы и подошли к более интересному, к практике. Посмотрим как можно решить задачу регрессии с помощью нейронных сетей (neural networks). Реализовывать все будем на языке программирования Python, для создания сети используем библиотеку глубокого обучения PyTorch.
Генерация исходных данных
Входные данные
Генерация данных
N = 3000 # размер данных
IN_DIM = 1
OUT_DIM = IN_DIM
x = np.random.uniform(-15., 15., (IN_DIM, N)).T.astype(np.float32)
noise = np.random.normal(size=(N, 1)).astype(np.float32)
y = 0.5*x+ 8.*np.sin(0.3*x) + noise # формула 3
x_train, x_test, y_train, y_test = train_test_split(x, y) #разобьем на тренировочные и тестовые данные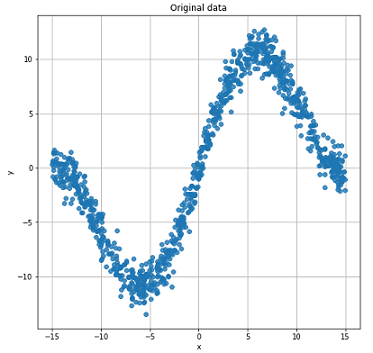
График полученных данных.
Построение сети
Создадим обычную сеть прямого распространения (feed forward neural network или FFNN).
Построение FFNN
class Net(nn.Module):
def __init__(self, input_dim=IN_DIM, out_dim=OUT_DIM, layer_size=40):
super(Net, self).__init__()
self.fc = nn.Linear(input_dim, layer_size)
self.logit = nn.Linear(layer_size, out_dim)
def forward(self, x):
x = F.tanh(self.fc(x)) # формула 4
x = self.logit(x)
return xНаша сеть состоит из одного скрытого слоя размерностью 40 нейронов и с функцией активации — гиперболический тангенс:
Обучение и получение результатов
В качестве оптимизатора будем использовать AdamOptimizer. Количество эпох обучения = 2000, скорость обучения (learning rate или lr) = 0.1.
Обучение FFNN
def train(net, x_train, y_train, x_test, y_test, epoches=2000, lr=0.1):
criterion = nn.MSELoss()
optimizer = optim.Adam(net.parameters(), lr=lr)
N_EPOCHES = epoches
BS = 1500
n_batches = int(np.ceil(x_train.shape[0] / BS))
train_losses = []
test_losses = []
for i in range(N_EPOCHES):
for bi in range(n_batches):
x_batch, y_batch = fetch_batch(x_train, y_train, bi, BS)
x_train_var = Variable(torch.from_numpy(x_batch))
y_train_var = Variable(torch.from_numpy(y_batch))
optimizer.zero_grad()
outputs = net(x_train_var)
loss = criterion(outputs, y_train_var)
loss.backward()
optimizer.step()
with torch.no_grad():
x_test_var = Variable(torch.from_numpy(x_test))
y_test_var = Variable(torch.from_numpy(y_test))
outputs = net(x_test_var)
test_loss = criterion(outputs, y_test_var)
test_losses.append(test_loss.item())
train_losses.append(loss.item())
if i%100 == 0:
sys.stdout.write('\r Iter: %d, test loss: %.5f, train loss: %.5f'
%(i, test_loss.item(), loss.item()))
sys.stdout.flush()
return train_losses, test_losses
net = Net()
train_losses, test_losses = train(net, x_train, y_train, x_test, y_test)Теперь посмотрим на результаты обучения.
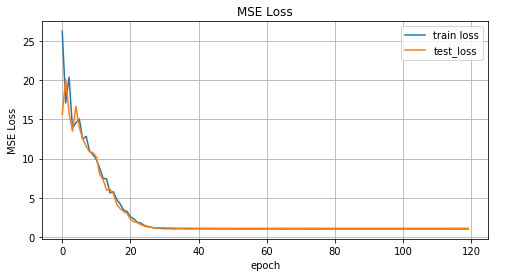
График значений MSE функции в зависимости от итерации обучения, на графике значения для тренировочных данных и тестовых данных.
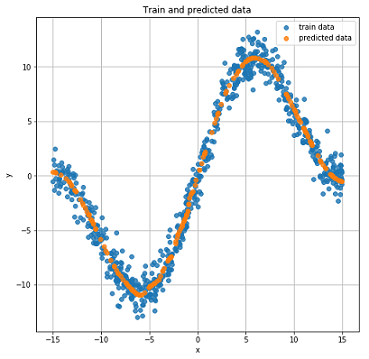
Реальные и предсказанные результаты на тестовых данных.
Инвертированные данные
Усложним задачу и инвертируем данные.
Инвертирование данных
x_train_inv = y_train
y_train_inv = x_train
x_test_inv = y_train
y_test_inv = x_train
График Инвертированных данных.
Для предсказания
inv_train_losses, inv_test_losses = train(net, x_train_inv, y_train_inv, x_test_inv, y_test_inv)
График значений MSE функции в зависимости от итерации обучения, на графике значения для тренировочных данных и тестовых данных.
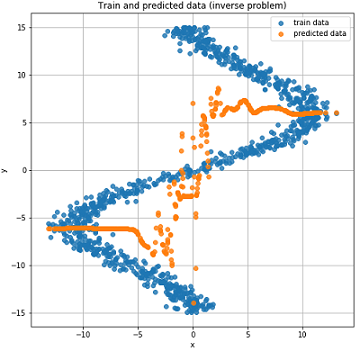
Реальные и предсказанные результаты на тестовых данных.
Как можно видеть из графиков выше наша сеть вообще никак не справилась с такими данными, она просто не в состоянии их предсказать. А все это случилось потому что в такой инвертированной задаче для одной точки
Mixture Density Network
Начинается самое интересное! Что же такое Mixture Density Network (далее MDN или MD сеть)? В общем эта некая модель, которая способна моделировать несколько распределений сразу:
Еще пару слов о
Фух, опять эта математика, давайте уже что то напишем. И так, начнем реализовывать сеть. Для нашей сети возьмем
self.fc = nn.Linear(input_dim, layer_size)
self.fc2 = nn.Linear(layer_size, 50)
self.pi = nn.Linear(layer_size, coefs)
self.mu = nn.Linear(layer_size, out_dim*coefs) # mean
self.sigma_sq = nn.Linear(layer_size, coefs) # varianceОпределим выходные слои для нашей сети:
x = F.relu(self.fc(x))
x = F.relu(self.fc2(x))
pi = F.softmax(self.pi(x), dim=1)
sigma_sq = torch.exp(self.sigma_sq(x))
mu = self.mu(x)Напишем функцию ошибки или loss function, формула (5):
def gaussian_pdf(x, mu, sigma_sq):
return (1/torch.sqrt(2*np.pi*sigma_sq)) * torch.exp((-1/(2*sigma_sq)) * torch.norm((x-mu), 2, 1)**2)
losses = Variable(torch.zeros(y.shape[0])) # p(y|x)
for i in range(COEFS):
likelihood = gaussian_pdf(y, mu[:, i*OUT_DIM:(i+1)*OUT_DIM], sigma_sq[:, i])
prior = pi[:, i]
losses += prior * likelihood
loss = torch.mean(-torch.log(losses))Полный код построения MDN
COEFS = 30
class MDN(nn.Module):
def __init__(self, input_dim=IN_DIM, out_dim=OUT_DIM, layer_size=50, coefs=COEFS):
super(MDN, self).__init__()
self.fc = nn.Linear(input_dim, layer_size)
self.fc2 = nn.Linear(layer_size, 50)
self.pi = nn.Linear(layer_size, coefs)
self.mu = nn.Linear(layer_size, out_dim*coefs) # mean
self.sigma_sq = nn.Linear(layer_size, coefs) # variance
self.out_dim = out_dim
self.coefs = coefs
def forward(self, x):
x = F.relu(self.fc(x))
x = F.relu(self.fc2(x))
pi = F.softmax(self.pi(x), dim=1)
sigma_sq = torch.exp(self.sigma_sq(x))
mu = self.mu(x)
return pi, mu, sigma_sq
# функция плотности вероятности для нормального распределения
def gaussian_pdf(x, mu, sigma_sq):
return (1/torch.sqrt(2*np.pi*sigma_sq)) * torch.exp((-1/(2*sigma_sq)) * torch.norm((x-mu), 2, 1)**2)
# функция ошибки
def loss_fn(y, pi, mu, sigma_sq):
losses = Variable(torch.zeros(y.shape[0])) # p(y|x)
for i in range(COEFS):
likelihood = gaussian_pdf(y,
mu[:, i*OUT_DIM:(i+1)*OUT_DIM],
sigma_sq[:, i])
prior = pi[:, i]
losses += prior * likelihood
loss = torch.mean(-torch.log(losses))
return lossНаша MD сеть готова к работе. Почти готова. Осталось ее обучить и посмотреть на результаты.
Обучение MDN
def train_mdn(net, x_train, y_train, x_test, y_test, epoches=1000):
optimizer = optim.Adam(net.parameters(), lr=0.01)
N_EPOCHES = epoches
BS = 1500
n_batches = int(np.ceil(x_train.shape[0] / BS))
train_losses = []
test_losses = []
for i in range(N_EPOCHES):
for bi in range(n_batches):
x_batch, y_batch = fetch_batch(x_train, y_train, bi, BS)
x_train_var = Variable(torch.from_numpy(x_batch))
y_train_var = Variable(torch.from_numpy(y_batch))
optimizer.zero_grad()
pi, mu, sigma_sq = net(x_train_var)
loss = loss_fn(y_train_var, pi, mu, sigma_sq)
loss.backward()
optimizer.step()
with torch.no_grad():
if i%10 == 0:
x_test_var = Variable(torch.from_numpy(x_test))
y_test_var = Variable(torch.from_numpy(y_test))
pi, mu, sigma_sq = net(x_test_var)
test_loss = loss_fn(y_test_var, pi, mu, sigma_sq)
train_losses.append(loss.item())
test_losses.append(test_loss.item())
sys.stdout.write('\r Iter: %d, test loss: %.5f, train loss: %.5f'
%(i, test_loss.item(), loss.item()))
sys.stdout.flush()
return train_losses, test_losses
mdn_net = MDN()
mdn_train_losses, mdn_test_losses = train_mdn(mdn_net, x_train_inv, y_train_inv, x_test_inv, y_test_inv)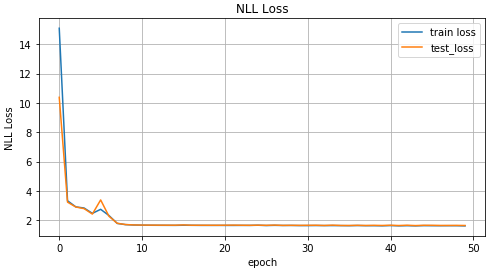
График значений loss функции в зависимости от итерации обучения, на графике значения для тренировочных данных и тестовых данных.
Так как наша сеть выучила значения среднего для нескольких распределений то давайте на это посмотрим:
pi, mu, sigma_sq = mdn_net(Variable(torch.from_numpy(x_test_inv)))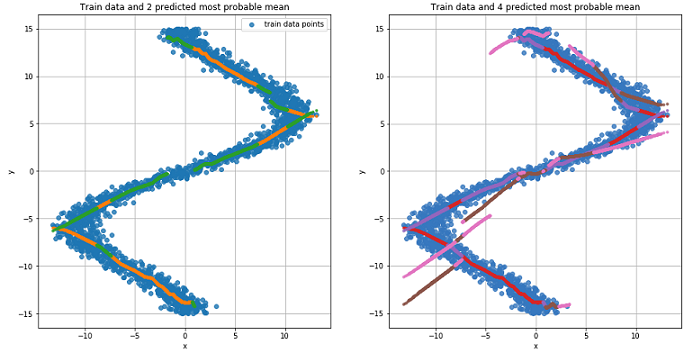
График для двух наиболее вероятных значений среднего для каждой точки (слева). График для 4 наиболее вероятных значений среднего для каждой точки (справа).
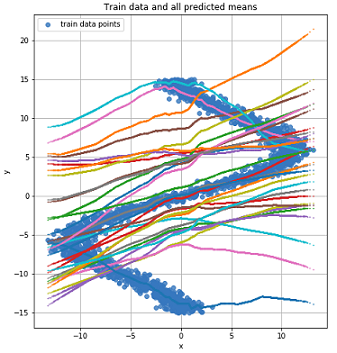
График для всех значений среднего для каждой точки.
Для предсказания данных будем случайно выбирать несколько значений
Предсказание результата
def rand_n_sample_cumulative(pi, mu, sigmasq, samples=10):
n = pi.shape[0]
out = Variable(torch.zeros(n, samples, OUT_DIM))
for i in range(n):
for j in range(samples):
u = np.random.uniform()
prob_sum = 0
for k in range(COEFS):
prob_sum += pi.data[i, k]
if u < prob_sum:
for od in range(OUT_DIM):
sample = np.random.normal(mu.data[i, k*OUT_DIM+od], np.sqrt(sigmasq.data[i, k]))
out[i, j, od] = sample
break
return out
pi, mu, sigma_sq = mdn_net(Variable(torch.from_numpy(x_test_inv)))
preds = rand_n_sample_cumulative(pi, mu, sigma_sq, samples=10)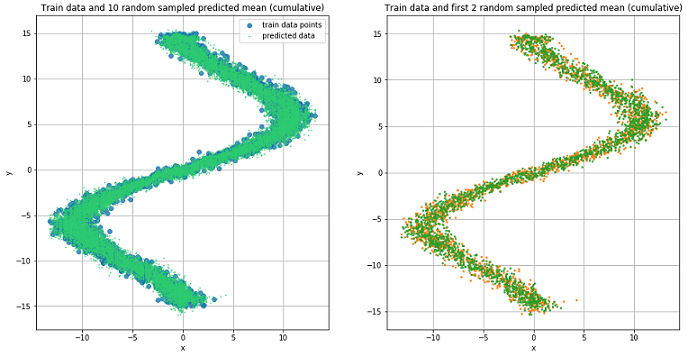
Предсказанные данные для 10 случайно выбранных значений
Из рисунков видно, что MDN отлично справилась с «обратной» задачей.
Использование более сложных данных
Посмотрим как наша MD сеть справится с более сложными данными, например спиральными данными. Уравнение гиперболической спирали в декартовых координатах:
Генерация спиралевидных данных
N = 2000
x_train_compl = []
y_train_compl = []
x_test_compl = []
y_test_compl = []
noise_train = np.random.uniform(-1, 1, (N, IN_DIM)).astype(np.float32)
noise_test = np.random.uniform(-1, 1, (N, IN_DIM)).astype(np.float32)
for i, theta in enumerate(np.linspace(0, 5*np.pi, N).astype(np.float32)):
# формула 6
r = ((theta))
x_train_compl.append(r*np.cos(theta) + noise_train[i])
y_train_compl.append(r*np.sin(theta))
x_test_compl.append(r*np.cos(theta) + noise_test[i])
y_test_compl.append(r*np.sin(theta))
x_train_compl = np.array(x_train_compl).reshape((-1, 1))
y_train_compl = np.array(y_train_compl).reshape((-1, 1))
x_test_compl = np.array(x_test_compl).reshape((-1, 1))
y_test_compl = np.array(y_test_compl).reshape((-1, 1))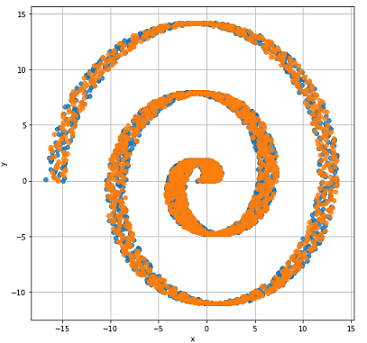
График полученных спиралевидных данных.
Ради интереса посмотрим как обычная Feed-Forward сеть справится с такой задачей.
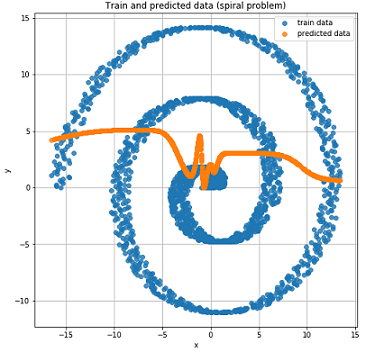
Как это и было ожидаемо Feed-Forward сеть не в состоянии решить задачу регрессии для таких данных.
Используем, ранее описанную и созданную, MD сеть для обучения на спиралевидных данных.
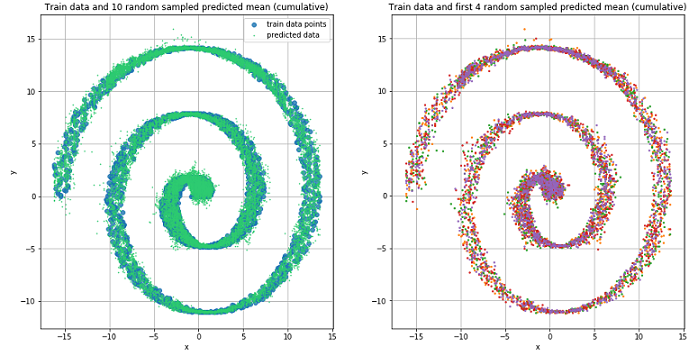
Mixture Density Network и в данной ситуации отлично справилась.
Заключение
В начале данной статьи мы вспомнили основы линейной регрессии. Увидели что общего между нахождением среднего для нормального распределения и MSE. Разобрали как связаны NLL и cross entropy. И самое главное мы разобрались с моделью MDN, которая способна обучаться на данных, полученных из смешанного распределения. Надеюсь статья получилась понятной и интересной, несмотря на то, что было немного математики.
Полный код можно посмотреть на GitHub.
















