Ну заяц погоди! Или противоракетная оборона для самых маленьких евреев и не только. Часть 1

Введение

В тексте на школьном примере демонстрируется вся красота структурного моделирования технических систем. Рассматривается задача погони волка за зайцем которая на самом деле является задачей перехвата любых целей в многомерном пространстве. Объясняем на пальцах, для самых маленьких, как работает система противоракетной обороны Израиля. Мне кажется, что у меня получилось объяснить способы решения системы алгебраический и дифференциальных уравнений маленькому человеку, которые еще не знает что такое производная или большу человеку кoторый и не знал, и уже забыл об этом. Один знакомы финансист прочитав этот текст, бросил дебет с кредитом и банковские проводки и попросился работать инженером, потому что ему вдруг стало все понятно.

Лирическое отступление

Есть в нашей стране товарищи, которые нам не совсем товарищи, а совсем даже наоборот – продажные наймиты мировой буржуазии. К сожалению, немало таких и среди отечественной профессуры, даже в ведущих вузах. Так вот, эти (которые нам не товарищи), нимало не смущаясь, с лицом УГ заявляют примерно следующее:

«Импортозамещение провалилось, мы и дальше будем учить студентов MATLAB Simulink. Потому что промышленность требует, чтобы наши студенты знали MATLAB» 

В такие моменты начинаешь понимать не только логику сталинских репрессий и борьбы с преклонением перед западом, но даже логику товарища Мао: «огонь по штабам!» Хуйвейбины и все такое. А иногда, в минуты слабости, даже начинаешь понимать логику «Красных Кхмеров», которые просто мотыгами всех, кто грамотный и в очках, уничтожали без разбора.  Но это не наши методы. Как говорил товарищ Ленин: «Мы пойдем другим путем!» 

К счастью, есть у нас в России и другие примеры, которые на фоне всего этого смотрятся как луч света в темном царстве и пророки в своем отечестве. Ради таких Преподавателей с большой буквы можно простить советско-российской системе образования все остальное что она породила и порождает.  Один из таких великих – это Очков Валерий Федорович. Я его полюбил, еще будучи студентом МГТУ им. Баумана. Для одной из курсовой мне понадобилось разобраться с MathCAD, а именно, узнать, каким образом составляются программы. В киоске Бауманки я увидел книгу «МathCAD 5.0». Полистав ее, убедился, что пример с программированием там есть, и купил. В те далекие времена дебильников у студентов еще не было, поэтому по пути из Бауманки в свое Замкадье, я открыл купленную книжку. Открыл и обалдел! Это был вынос мозга.

Книжка, посвященная работе в математической программе, читалась как художественный роман. Я прочитал ее от корки до корки, даже без компьютера, за одну поездку.  

Можно, конечно, предположить, что тогда я был немного больной на всю голову, но уровень книг Валерия Федоровича по MatCAD, признан авторами самого MatCAD, которые пригласили нашего писателя в Бостон, выдали «бочку варенья и корзину печенья», а английские версии его книг с успехом до сих пор продаются на мировых площадках.

Казалось бы, после введения санкций на техническое сотрудничество автор мировых бестселлеров по импортной инженерной программе должен впасть в уныние и проклинать импортозамещение. Но нет, Валерий Федорович просто взял отечественную аналогичную программу SMath Studio и спокойно пишет такие же крутые книги на базе отечественного ПО.  Доказывая, что нормальные ученые и преподаватели находят замену сдристнвушим западным разработчикам, что не может не радовать.

«Я знаю — город будет, я знаю — саду цвесть, когда такие люди в стране в советской есть!» 

Валерий Федорович предложил мне рассмотреть задачу о погоне. В исходной версии по кругу бежит заяц с постоянной заданной скоростью. Из любой точки запускается собака, которая также с постоянной скоростью бежит за зайцем. Задача: рассчитать направления движения собаки, время и точку перехвата. Это же самая прямая задача для среды структурного моделирования технических систем.

Ну заяц погоди!

В исходной версии по кругу бежит заяц с постоянной заданной скоростью. Из любой точки запускается собака, которая также с постоянной скоростью бежит за зайцем. Задача: рассчитать направления движения собаки, время и точку перехвата. Это же самая прямая задача для среды структурного моделирования технических систем.

Начнем с простого: заяц бежит по кругу. Тут все просто. Нужно нарисовать круг с заданными параметрами без всяких затей.

Функция зависимости угла от времени для заданного радиуса и скорости известна, смотри рисунок:

Зная угол и радиус, легко находим положение зайца на плоскости - координаты Х и Y. Когда у нас SMath, то у нас все просто: записываем формулу и получаем ответы. Но мы не ищем легких путей, и у нас среда структурного моделирования. Что это за зверь и с чем его едят? 

Структурное моделирование для самых маленьких

 Структурное моделирование – это когда мы модель собираем не в формулах, а в графическом виде. Модель строится в виде функционально-блочной диаграммы (это такие блоки со стрелками, как нас учит кибернетика, в прошлом лже-наука и продажная девка мировой буржуазии). 

Кибернетика (от греч. kybernetike — «искусство управления», от kybernáo — «правлю рулём, управляю») — наука об управлении, связи и переработке информации.

Основной объект исследования в кибернетике — кибернетические системы, которые представляют собой множество взаимосвязанных объектов, способных воспринимать, запоминать и перерабатывать информацию, а также обмениваться информацией. Примеры кибернетических систем: автоматические регуляторы в технике (например, автопилот или регулятор, обеспечивающий поддержание постоянной температуры в помещении), электронные вычислительные машины (ЭВМ), человеческий мозг, биологические популяции, человеческое общество.

В этой науке любая система представлена вот примерно в таком виде, как на рисунке 2:

Вот мы и будем создавать подобные диаграммы.

Функционально-блочная схема состоит из блоков, соединенных линиями связи. 

Линия связи – это как переменные в языке программирования. Они всегда содержат в себе одно или несколько (вектор или матрицу) чисел. И служат для передачи этих чисел между блоками.

Блоки выполняют математические операции над числами. Каждый блок берет данные из линии связи на входе что-то вычисляет и выдает результат вычислений в линию связи на выходе.

Если у блока нет входа, то он просто является «источником». Источник просто выдает на выход числа по какому-то закону. Если у блока нет выхода, он просто берет данные с линии и что-то с ними делает, например, скалывает их в файл или выводит на график, а может и отправляет в ЦРУ или Моссад по интернету (такие блоки тоже есть)

У каждого блока есть набор свойств, которые мы можем менять, чтобы влиять на то, что именно блок считает.

Модельное время

Вся это графическая схема описывает состояние объекта в любой момент времени. Система моделирования SimInTech позволяет запустить время и посмотреть, как вся эта система себя ведет во времени. Для это мы задаем начальное состояние, а потом запускаем расчет по времени. В процессе расчета последовательно, с заданным шагом, происходит расчет всех блоков. На каждом временном шаге каждый блок схемы берет значение со входа (или не берет, если это источник), выполняет расчет и выдаёт на выход. Мы получаем новое значение и делаем следующий шаг по времени, и можем наблюдать за процессом в модельном времени. Это и называется моделирование процессов. 

Теперь, когда вы знакомы с бывшей продажной девкой кибернетикой, перейдем непосредственно к моделированию. Начнем рассмотрение с модели зайца в среде SimInTech. Здесь у нас есть схемное окно, где из блоков собирается функционально-блочная диаграмма. 

Блоки разные, на любой вкус и цвет, как фломастеры, находятся в палитре блоков: 

Из схемного окна вызывается страница скрипта проекта, где можно задать переменные, как в любом языке программирования.

В главном скрипте проекта задаем в виде констант радиус и две скорости, для зайца и для волка. Здесь мы задаем их в численном виде и в дальнейшем можем использовать уже не числа, а имена R, v_z и v_s.

Блоки, поставленные на схему, можно настраивать. Для этого у них есть окно редактирования. Посмотрим, например, на блок “Линейный источник”. Он не имеет входа, а выдает на выходе значение равное, где: , где:

– модельное время;

– коэффициенты, которые мы задаем в свойствах блока.

Для коэффициентамы задаем 0 , начало будет с 0.

Для коэффициентау нас формула v_z/R – угловая скорость зайца. Записав эту формулу в столбец «Формула», мы в столбце «Значение» получаем число, равное 5/700 = 0.007142857143.  

Во время расчета по мере увеличения времени блок будет выдавать угол зайца в каждый момент времени, увеличивая его с постоянной угловой скоростью, соответствующей заданной в глобальных константах.

Далее на схеме у нас стоят блоки синус и косинус, которые, получив угол поворота, рассчитывают положение координаты зайца. Для этого у них в свойствах в столбце в качестве амплитуды указан Rрадиус круга, по которому бегает заяц. 

Данный блок выполняет следующие вычисления: , где:

- выход блока (то, что блок выдает на линию связи);

- выход блока (то, что блок забирает с линии связи);

- амплитуда; - частота; - фаза. Эти свойства которой задаются для блока.

В нашем случае 

А поскольку на линии связи входа  у нас как угол, который выдает линейный источник, то мы получаем как раз то, что нам нужно, чтобы посчитать координату зайца. 

То же самое для , только мы в параметрах блока тип функции меняем на косинус.

Последний блок на схеме – это фазовый портрет, который забирает с линии значения координат зайца и и строит траекторию движения.

Наша схема простая и понятная, но можно сделать ее еще более наглядной. Для этого мы можем подписать блоки, записав выражения, которые они вычисляют. 

Для этого в палитре блоков есть панель примитивов, откуда можно взять подпись и поставить в любое место схемы.

В этом случае мы прямо на схеме видим выражение, которое рассчитывается в каждом блокe cучетом принятых в модели обозначений. Например, у нас R, v_z

Чтобы запустить расчет, нам нужно настроить наши шаги моделирования. Нажимаем кнопку с молотком и отверткой и получаем окно настройки проекта:

Для модели зайца выберем шаг выберем Минимальный шаг и Максимальный шаг равным 1-ой секунде и метод интегрирования (расчета) Эйлера (в этом методе как раз постоянный шаг).

Чтобы заяц успел пробежать круг, конечное время расчета поставим 1000 секунд.

На верхней панели у нас есть кнопки управления расчетом. Если нажать на кнопку с секундомером, то модель рассчитает начальное положение и остановится, либо выдаст ошибку, если вы не задали какое-то значение или не соединили линии связи с блоками.

Там же есть кнопка отображения значений на линии связи. В этом случае у каждого блока на линии связи у выхода будет отображаться значение, которое в данный момент содержится в линии.

Нажав на кнопку с секундомером, мы можем проверить нашу схему.  Координаты зайца: начальный угол 0, sin (0) =0 и Yз =0, для cos(0) = 1 и Xз = R =700 все верно.

Далее можно сделать один шаг – кнопочка с желтым треугольником. Время увеличится на один шаг, заданный в параметрах расчета (у нас – 1 секунда), выполнятся вычисления всех блоков, и расчет снова встанет на паузу, ожидая дальнейших распоряжений.

Если нажать на зеленую кнопку, то расчет запустится без пауз с заданным шагом до конечного времени 1000 секунда. А фазовый портрет нам изобразит идеальный круг.

Поздравляю, модель зайца побежала по кругу!

Пиши, сокращай

Попробуем немного упростить схему. Как был сказано ранее, в линии может быть не только одно число, а вектор или даже матрица и блоки могут обрабатывать эти вектора, так же, как и числа. В нашей модели зайца было бы удобно, что бы в лини сразу были координаты зайца вместе [X,Y]. Из геометрии мы знаем, что синус, угла равен косинусу этого же угла, но повернутого на 90 град.

Давайте вместо двух блоков, соs и sin будем использовать один, которые выдаст нам два нужных значения. Для этого настроим блок источник так, чтобы у него вместо одного числа в линию выдавался вектор из двух чисел. Для этого достаточно в свойствах, вместо одного числа указать в квадратных скобках, через запятую несколько значений.  «Коэффициент при t» в столбце формула зададим значение [v_z/R, v_z/R], в столбце значения появится вектор из двух одинаковых числе. Если числа одинаковые, то в столбце Формула можно задать выражение, 2# v_z/R, где 2 – количество значений в векторе. Как мы это сделали для свойства «Свободный член»  2#0

Если сейчас нажать на кнопку инициализации, то мы увидим, что на выходе из блока в линии появилось два значения, и блоки синус и косинус тоже выдают по два значения. Получив два угла, они выдают два синуса и косинуса, но это не совсем то, что нам нужно. 

Давайте поменяем свойства блока косинус, так что бы получив на вход, два одинаковых значения угла, он выдал нам разные координаты - X и Y зайца. Для этого в свойстве «Фаза»  в столбце «Формула», запишем выражение [0,pi/2]. Таким образом наш блок для первого числа, полученного с входного значения, не будет изменять способ расчета. Первое число как и ранее будет считать косинус, а к второму числу будет добавлен угол :

В итоге мы получим вместо косинуса, синус того же угла, и второе число на выходе даст нам значение Y

Если инициализировать проект, у на в линии выхода из блока синуса будет [700, 4.286XXXE-14]. Второе число очень маленькое и близкое к 0. Можно принять за 0 в пределах точности вычисления.

Таки образом, один блок будет рассчитывать и синус, и косинус и второй блок нам не нужен, а для того, чтобы построит фазовый портрет мы добавим блок, разбирающий вектор на два числа.

Если мы запусти на расчет, то увидим, что фазовый портрет не изменился заяц благополучно бегает по кругу.

С зайцем разобрались тут все просто. Рисуем круг по формуле. 

Волка ноги кормят

Волку нужно не просто бессмысленно бежать, куда глаза глядят, а бежать за зайцем. А значит, мы должны постоянно менять направление волка. Тут-то и поможет нам бывшая лженаука кибернетика. Смотрим на картинку. Регулирующее устройство 1 – это система наведения волка. Она должна выработать воздействие 3 на объект управления 2 – волка так, чтобы он двигался в сторону зайца. Это будет выход 4. Чтобы навести зайца, нам нужно получить положение волка по каналу обратной связи 5 и положение зайца 6.

Модель волка будет на базе интегратора. 

Что такое интегратор человек или лошадь?

Для самых маленьких, кто еще не изучал теорию автоматического управления, и больших, которые ее не помнили или уже забыли, Интегратор — это такой блок, который на вход получает скорость объекта, а на выходе рассчитывает расстояние, которое пройдет объект за данное время.  Объясним на пальцах:

Представим, что у вас есть автомобиль, который движется со скоростью v = 40 км/час. Как узнать, на какое расстояние S он переместится за время t = 5 часов? Ответ знает каждый школьник: нужно умножить на время на скорость. 

км. Ответ верный, но не правильный. В жизни никогда 200 км прямой дороги не бывает, всегда есть горки подъёмы и спуски.

Если отправим этот же самый автомобиль по холмистой дороге, где он будет ехать медленнее в горку и быстрее с горки, где он окажется через 5 часов? 

Соберем модель, в которой постоянная скорость 40 км/час складывается с синусоидой с амплитудой 20, зададим конечное время 20 и построим график. 

Видно, что у нас сначала автомобиль разгоняется до 60 км/час, потом тормозиться до 20 км/час, потом начинает разгоняться, но время заканчивается. Это простой случай, а в реальности автомобиль вообще может остановиться на заправку или постоять час в пробке. 

Ровно такая же задача возникает, если мы рассматриваем модель бассейна, в который втекает или из которого вытекает вода. Пока расход воды постоянный, проблем нет. Расход умножаем на время и получаем массу воды. Как только расход начинает меняться во времени, простые школьные методы уже не работают.

Как в этом случае считать путь? На наше счастье, в славном городе Санкт-Петербурге в 1786 году наш славный ученых Леонард Эйлер предложил решение в своей работе «Интегральное исчисление».

Если сильно упростить его метод, то он предложил в расчете разбить все время процесса на равные интервалы. И считать, что в пределах одного интервала скорость не меняется. Тогда на каждом маленьком интервале мы можем посчитать скорость по формуле где:

расстояние, пройденное за временной интервал;

скорость на интервале, у каждого интервала она будет своя;

время интервала, одинаковое для всех интервалов.

Понятно, что само решение приблизительное, но, чем меньше шаг интервала, тем точнее решение.

После этого нужно просто сложить все полученные расстояния, и мы получим полный путь. Наблюдательные читатели наверняка заметили, что у нас в этом методе появился шаг интегрирования. И это совсем не случайно. Давайте для нашей модели автомобиля на холмистой дороге установим минимальный и максимальный шаг интегрирования, равным 1.  Это грубое приближение, но для понимания алгоритма точность сейчас не так важна.

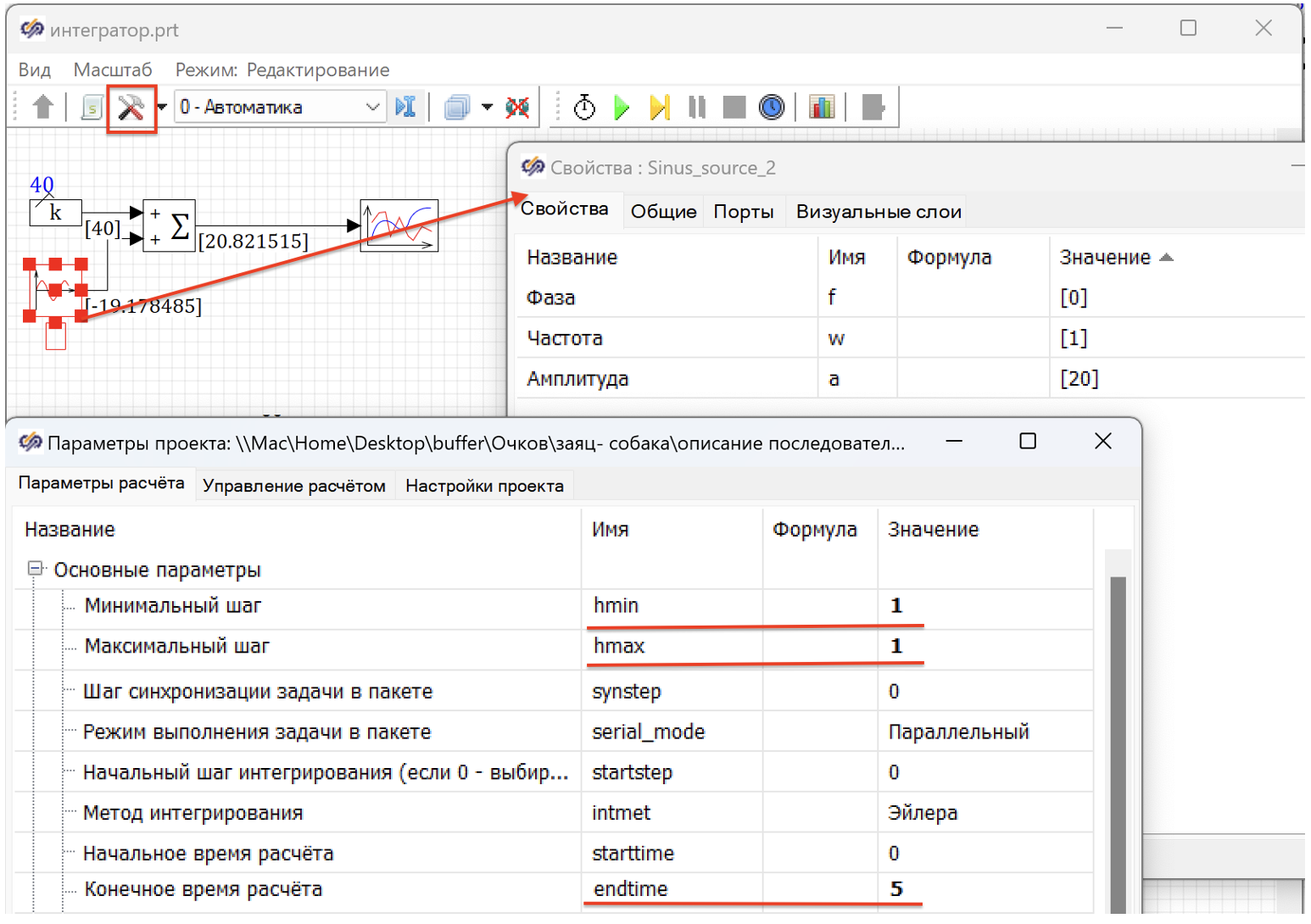
И, кстати, вы заметили, что метод интегрирования у нас установлен метод Эйлера. Это тоже не совпадение. Это именно тот самый метод, изобретенный в Санкт-Петербурге более чем 250 лет назад, и, заметьте, без всяких компьютеров. 

Запустим на расчет и получим вместо плавной кривой, вот такую ломаную:

РДля каждого шага у нас есть скорость, которую мы можем использовать для расчета расстояния на каждом участке. Соберем схему, которая реализует метод Эйлера.

Добавим блок «Шаг интегрирования», который выдает время шага. Умножим скорость на этот шаг интегрирования, у нас получится путь за этот интервал:

- это путь, который пройдет автомобиль за интервал времени .

Остается теперь сложить все пути за все время расчета. Для этого мы используем блок «Задержка на шаг интегрирования». Этот блок, получив значение на входе, запоминает его, а на выход выдает значения с предыдущего шага расчета.  (Для первого шага в блоке нужно указать начальное состояние = 0)

Установим сумматор, который будет складывать единичный интервал с уже пройдённым путем:

и эту сумму направим в блок «Задержка на шаг интегрирования». Этот блок запомнит сумму и выдаст ее на следующем шаге. Сумму пройденного пути мы заберем с выхода этой задержки.

Таким образом, на выходе из блока задержки у нас будет всегда суммарный путь.

Сделаем инициализацию. схемы и подсветим значения на линиях. Посмотрим, что у нас получилось:

В начальный момент времени источник синусоидального сигнала выдает 0 и скорость после сумматора Vi = 40. Шаг у нас установлен 1, поэтому путь за интервал тоже равен 40. В сумматоре этот путь складывается с начальным значением задержки = 0, итого путь за интервал равен 40. И этот будущий путь запоминается в задержке, а при t = 0 сама задержка выдает 0 – начальное значение, что верно. Какой может быть путь, когда время равно 0? Правильно нулевой!

Сделаем 1 шаг по времени, нажав кнопку с желтым треугольником.

Источник синусоидального сигнала выдал 16.82942, общая скорость в этот момент времени стала 56.823942, путь за интервал увеличился= 56.823942 x 1 = 56.823942.

В сумматоре новый путь сложился с уже пройдённым 40, таким образом общий путь для следующего момента времени 40 + 56.823942 = 66.823942, и мы его запомнили в задержке, а сохраненный ранее путь из задержки 40 переместился на выход. 

И мы получили путь 40 за 1 времени, именно то, что требует метод.

Можно повторить шаги 5 раз и получить общий путь, посчитанный методом Эйлера.

Если у вас получилось такое решение, то поздравляю! Вы не только повторили метод Эйлера, изобретенный 250 лет назад, но и поняли, как работает блок интегратор! Все, что мы с вам нарисовали в схеме, можно получить, поставив один единственный блок – интегратор. Результат будет точно такой же в конце расчета.

И не только в конце расчета! График процесса тоже совпадет по точкам!

Если поменять шаг интегрирования, скажем до 0.01, то мы получим более точное плавное решение. При этом результат вычисления пути интегратором полностью совпадает с вычислением пути методом Эйлера.

Таким образом, мы сейчас показали, как работает волшебный блок-интегратор, на вход которого подается скорость, на выходе получается путь. Точно также он работает, если у вас есть расход в бассейне: интегратор посчитает массу воды в бассейне и вообще любые подобные задачи. 

Выражаясь научным языком, если у вас есть производная какого-либо параметра процесса, то блок-интегратор рассчитает это самый параметр.

Посмотрим на свойства интегратора, их всего два.

Начальные условия – 0, позиция, с которой начинается движение в нашем случае 0.

Коэффициенты усиления – 1, коэффициент, на который умножается входное значение. 

В нашей модели мы использовали 1 и подавали скорость в качестве входного воздействия.  Но можно задать скорость в блоке, а на вход подавать «управляющее воздействие» - коэффициент скорости. 

Например, можно задавать ступенчатое увеличение скорости с 20 до 40, а можно задать 40 в виде коэффициента усиления, а управление задавать ступенчатый воздействие с 0.5 до 1. В обоих случаях результат будет идентичным. 

Поскольку по условию задачи была задана скорость волка, то мы будем использовать управляющее воздействие, тем более кибернетика зря не посоветует.

Как было показано выше, между блоками по линии связи может предаваться не одно число, а вектор. Также и интегратор может одновременно считать несколько значений. Вот мы и будем выдавать ему управляющее воздействие, а скорость будет задана, как параметр интегратора волка.

Если рассмотреть скорость в двухмерном пространстве, то она раскладывается на две скорости Vx и  Vy, которые определяются углом направления.

Если скорость у нас задана по условию задачи, то нам достаточно в качестве управляющего воздействия задать косинус и синус угла направления на входе в интегратор. Такой интегратор и будет нашим волком.

Волка же ноги кормят, ему нужно не просто бежать, а бежать за зайцем. 

В нашем случае у нас интегратор должен рассчитывать расстояние в двухмерном пространстве X и У, а значит мы получаем вектор из двух значений. Далее этот вектор можно разобрать, как мы делали с зайцем, и пересобрать так, чтобы фазовый портрет отображал уже две траектории – зайца и волка.  

В качестве параметров интегратора задаем «Начальные условия» 2#0 [0,0] – стартует волк из нулевой точки. Коэффициент усиления обеспечит нам заданную скорость 2#V_s [5.3, 5.3]. см. рисунок:

Для проверки правильности работы подадим на вход источник ступенчатого сигнала 0 или 1, которые обеспечат движение с заданной скоростью по оси X или Y.

Начальные условия [1,0] – движение только по оси Х и нет движения по оси Y, через 100 секунд срабатывает ступенька и сигнал меняется на [0, 1] – движение по только по оси Y, по оси Х движения нет. 

Меняем время расчёта на 200 секунд и смотрим на результат:

Если все правильно, то видим, что за первые 100 секунд волк пробежал 530 метров по оси Х, что верно при скорости 5.3, далее по оси за следующие 100 секунд пробежал так же 530 метров, что тоже верно.

Значит наш волк-интегратор бегает с заданной скоростью. 

Куда бежать? Система наведения

Осталось только научить его бегать не просто так, а за зайцем. Для этого в интегратор мы должны подавать синус и косинус угла направления на зайца. 

Рассмотрим взаимное расположение зайца и волка в любой момент времени.

Координаты зайца мы рассчитали по его траектории, координаты волка у нас также известны на выходе из нашего интегратора.  А раз так, то мы можем вычислить расстояние между точками по всем осям и рассчитать синус и косинус угла. Схема расчета представлена на следующем рисунке:

Схему расчета синуса и косинуса достаточно просто собрать в SimInTech. Забираем положение зайца (Xз,Yз), отнимаем от него положение волка (Xв,Yв), получаем DX, DY, далее возводим в квадрат. Далее складываем, потом извлекаем корень (желтый прямоугольник на схеме), делаем обращение (1/D), после этого умножаем вектор на эту величину и получаем cos = DX * (1/D) и sin = DY * (1/D), после этого можно направлять волка в сторону зайца на каждом шаге. Как на следующем рисунке:

Устанавливаем время расчета 1000 и запускаем на расчет. И видим, что волк начинает гоняться за зайцем, стартуя из центра окружности.

Для того чтобы посмотреть наглядно, можно замедлить расчет. Для этого вызовите окно «Параметры расчета», установите «Синхронизацию с реальным временем» и коэффициент ускорения 40. 

После этого погоня волка за зайцем происходит прямо на ваших глазах.

На самом деле сейчас у нас на графике волк не только догоняет зайца, но даже обгоняет его. Давайте добавим остановку расчёта в момент, когда расстояние между волком и зайцем будет меньше 0.1 метра.

Для этого поставим на схему блок, который останавливает расчет, когда входной сигнал попадает в границу, установленную в блоке, и добавим сообщение, что зайца поймали. Так как у нас на схеме есть расчет расстояния, то мы легко можем его использовать для блока остановки расчета.

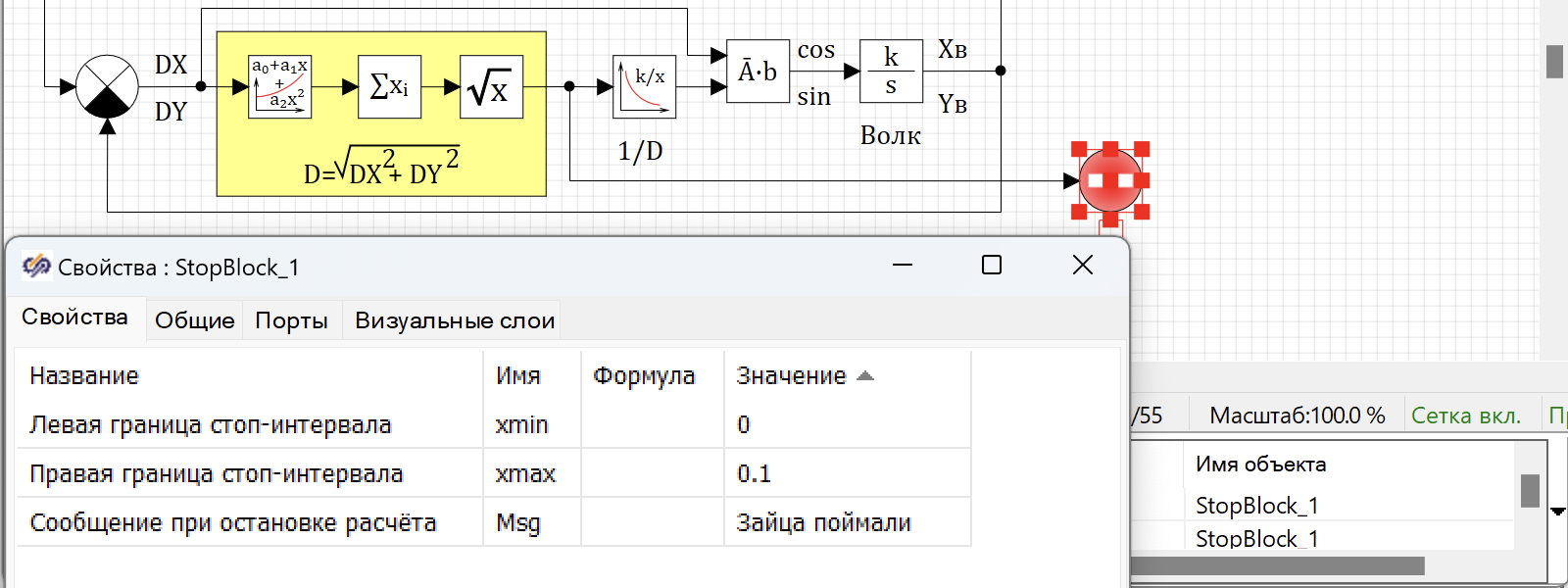
После этого волк перестает бегать по кругу, и расчет останавливается, как только волк догнал зайца. При этом мы видим в окне сообщения время, когда волк догнал зайца. 

В нашем случае волк догоняет зайца через 565 сек.

Структурное моделирование позволяет нам менять отдельные части модели. Например, пустить зайца по периметру квадрата и оценить, как волк сможет его поймать. Для этого создадим модель для зайца в виде интегратора, в свойствах которого задается скорость, а направление определяется ступенчатым источником. Запустим на расчет и убедимся, что наша модель волка ловит зайца, даже когда он бежит не по кругу, а по квадрату:

Для удобства использования модель в струкутрных схемах, и что бы модель выглядела так как от нас требует наука кибернетика, упакуем систему наведелния в отдельную субмодель. Тогда мы получим примерно такую схему волка с зайцем:

И теперь мы можем простой копипастой из одного волка сделать стаю волков. Можно поменять их скорости и исследовать особенности групповой охоты. Например на следующем рисунке у меня четыре медленных волка гоняются за одним быстрым зайцем:

Казалось бы, а причем здесь противоракетная оборона и евреи?

А вот об этом во второй части.

Подписывайтесь на канал Технолог Петухов там без цензуры.