Привет! Думаешь сможешь? Я думаю, что сможешь!.. Хотя, это не так важно - какой-то психопат запер котика в клетке и... Видимо, хочет сделать из него суп!.. Поэтому у нас каждый день на счету!!! Но ещё есть время...
В Австралии выпустили особую монету в честь 75-летия службы безопасности и разведки
2 мин
Новая монета в 50 центов несёт на себе секретное сообщение. Те, кому удастся расшифровать все четыре слоя загадок, могут претендовать на работу в агентстве безопасности и разведки Австралии (ASD).
Памятная монета тиражом 50 000 экземпляров выпущена сегодня в ознаменование 75-летия ASD. Хотя она не предназначена для обращения, монету можно купить на Королевском монетном дворе Австралии, чтобы попытаться взломать четыре уровня закодированных сообщений.
ШишНашКи
2 мин
Что тут? Математическая головоломка, немножко групповых перестановок, две задачи для узколобых и грань шутки. Beg your pardon, если эта головоломка придумана до меня и я жалкий невежа, вообразивший, что изобрел нечто новенькое. В случае лицензионной чистоты я нарекаю её ШишНашКи отныне и вовеки веков. Аминь.
По следам публикации
Человеческий гений в лице Mrrl решил задачу Бога в уме за 20 ходов.
Видео решения
Головоломка ассасина
Простой
9 мин
В 2014 году профессор математики Стэнфордского университета Марьям Мирзахани в одной из своих лекций упомянула интересную математическую головоломку, но не стала давать её решение. Спустя годы появились различные вариации задачи. Однако сначала речь пойдёт о первоисточнике.
Головоломка относится к классу так называемых «бильярдных задач», изучаемых в области динамических систем. Решение текущей задачи принадлежит профессору математики университета Джонса Хопкинса Эмили Рил.
Рассмотрим квадратную комнату в плоскости XY, и пусть A («ассасин») и T («цель») — две произвольные, но фиксированные точки внутри комнаты. Предположим, что комната схожа по физическим характеристикам с бильярдным столом, так что любой «выстрел» А рикошетит от стен, причём угол падения равен углу отражения. Можно ли заблокировать любой возможный «выстрел» А в Т, разместив конечное количество аналогичных по свойствам точек («телохранителей») в комнате?
Как я много раз не бросил разработку своей второй игры
15 мин
Картинка для привлечения внимания
Успокоившись после шока из-за того, что моя первая игра не взорвала интернет, я решил сделать еще одну. Первая мысль, с которой началась разработка второй игры, возникла в голове и без обдумывания стала краеугольным камнем в фундаменте игры: «если игра с бесконечным геймплеем не стала популярной, то нужно делать контенто-зависимую игру с уровнями».
Так как небольшой опыт создания игры у меня уже был, я вооружился не клавиатурой, как в прошлый раз, а карандашом и бумагой, и принялся «придумывать» игру. На разных листах А4 я записывал свои мысли по разным направлениям: игровые механики, сеттинг, интерфейс, правила, интересные мысли, запомнившиеся игры из детства и т. п.; при этом я параллельно шерстил Google Play Market в поисках вдохновения. В итоге, спустя несколько дней, было принято решение, что игра станет головоломкой, а именно — пазлом. За это время мой мозг и пальцы заскучали по программированию, в результате чего захотелось сделать хоть какой-нибудь прототип игры. Это сподвигло меня на более интенсивную проработку идеи пазла, и в итоге в качестве рабочего был принят вариант со следующими правилами: игровое поле состоит из квадратных кусочков пазла (далее они будут называться тайлами), на которых располагаются разноцветные линии; тайлы можно менять местами; цель игры: собрать пазл единственным образом, в котором линии одного цвета замкнуты в некий узор.
Головоломка-пазл для социальной сети
2 мин
Хочу представить хабрасообществу свою игру-пазл Разбитые дороги и поделиться результатами и выводами спустя 3 недели после запуска.
Данная короткая статья является логическим продолжением обзорно-мотивирующей статьи «Как я много раз не бросил разработку своей второй игры».
Данная короткая статья является логическим продолжением обзорно-мотивирующей статьи «Как я много раз не бросил разработку своей второй игры».
Квест в честь миллиона студентов на курсе для начинающих программистов
Простой
2 мин
Хабр, привет! Давно я не писал этих слов... На связи Тимур, автор серии курсов по программированию "Поколение Python". ?
Последний раз я публиковал статьи около 10 лет назад. За это время произошло много интересного, обязательно расскажу об этом, но позже. А пока хочу поделиться новостью: на нашем курсе для начинающих питонистов набралось более миллиона студентов. Это первый курс на платформе Stepik с таким количеством студентов.
Для нас и для Stepik это очень большое событие, и мы бы хотели разделить его с нашими студентами и со всеми, кто изучает программирование вообще. Поэтому мы проводим онлайн-квест: его участники будут решать задачи по программированию, математике, логике, а самые успешные и удачливые получат призы. Ведь программирование — это не только про написание кода, это про умение решать самые разные задачи.
Визуальный брутфорс на примере решения 3D-головоломки
5 мин
Когда-то давно друзья подарили вот такую головоломку:
Собрать её самостоятельно я так и не смог (всегда оставался один фрагмент). Посему было решено написать программу.
Для тех, кто не любит читать, решение доступно по ссылке (внимание, сильно нагружает процессор).
Собрать её самостоятельно я так и не смог (всегда оставался один фрагмент). Посему было решено написать программу.
Для тех, кто не любит читать, решение доступно по ссылке (внимание, сильно нагружает процессор).
Задача о минутах
4 мин
Жизнь, как говорится, лучший драматург. Так и задачи жизнь ставит не менее интересные, чем авторы занимательных книг по математике.
Буквально 2 дня назад одна, казалось бы, рутинная, неинтересная и лёгкая задача заставила меня понервничать и засомневаться в собственной адекватности восприятия реальности.
Буквально 2 дня назад одна, казалось бы, рутинная, неинтересная и лёгкая задача заставила меня понервничать и засомневаться в собственной адекватности восприятия реальности.
Интеллектуальный брутфорс: пишем головоломку и солвер для неё
16 мин
Перевод
Небольшое предисловие
В колледже я много играл в головоломки. В статье под головоломками я буду подразумевать очень узкое подмножество таких игр. Вот некоторые из примеров:
Также мне посчастливилось изучать структуры данных в Политехническом институте Ренсселера, где в то время студенты профессора Катлера (привет, Барб!) ежегодно участвовали в соревновании по написанию солвера головоломок. Каждый год игра менялась, и в мой год это была Ricochet Robots, которая по сути является головоломкой со скольжением по льду для нескольких игроков. Мне очень понравилось это задание (и я победил в соревновании!), после чего я продолжил участвовать в соревнованиях в качестве ассистента преподавателя.
Цель этой задачи заключалась в том, чтобы познакомить всех с рекурсией и поиском в глубину. Программе передавались исходное состояние игры, а также максимальная глубина рекурсии. Необходимо было вернуть или кратчайшее решение или все возможные решения минимальной длины. В соревнованиях игрокам могли или сообщать, или не сообщать предел глубины; кроме того, возможны были головоломки, не имеющие решения. Я многому научился и получил кучу удовольствия, так что, возможно, вам это тоже понравится.
Квест «В поисках сокровищ 21-го века»
3 мин
Раньше в поисках сокровищ, приключений и славы люди отправлялись в немыслимые путешествия, полные смертельных опасностей и трудностей, преодолевали горы, моря и пустыни, сражались и брали врагов хитростью, чтобы в конечном итоге где-то на краю земли обрести вожделенное богатство…
Времена изменились, общество стало более цивилизованным и развитым, а сокровища, некогда спрятанные или утерянные богачами и пиратами, почти все найдены…
В XXI веке наибольшая ценность для человека – информация. Владеющий нужной информацией может заполучить если не все, то очень многое! А что в наше время является самым масштабным хранилищем всей возможной информации? Правильно – Интернет!
Где-то на просторах сети есть один очень важный «ключ», открывающий дверь в мир полезных знаний. «Ключ» некогда был утерян, но что это за сокровище, которое невозможно найти? Ведь в сети найти можно все! Не опоздайте, «ключ» всего один и достаться он должен именно Вам!
Тетрис: история одной игры
22 мин
Сегодня «Тетрису» исполняется 38 лет, а потому неплохо будет вспомнить тот тернистый путь, через который прошла эта игра.
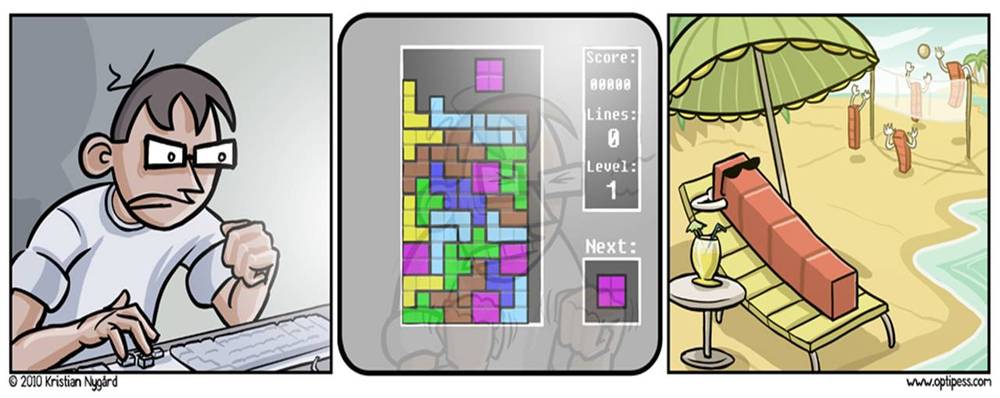
Я изобрел тетрис для собственного удовольствия. Только так и можно что-то изобрести, — Алексей Леонидович Пажитнов
Многое великое создаётся случайно, в рабочей рутине. Порой задумка создателя совсем не похожа на то, для чего вещь в итоге применят на практике. Скажем, для проверки гипотезы или забавы ради. Но судьба распоряжается так, что даже маленькая идея, реализованная во что-то весомое, становится мировым достоянием, вопреки всем планам и целям. Более того — она кардинально меняет жизни людей и даёт определенный виток развития по другим направлениям, задает тренд и становится хитом.
«Тетрис» как раз и стал такой задумкой, возникшей из случайности, почти как Вселенная, да. Головоломка, прогремевшая на весь мир, игра, чья история состояла из череды скандалов, интриг и судебных разбирательств, вполне себе достойна кинематографа. Можно сказать, что «Тетрис» не просто игра — это, по сути своей, целый культурный феномен, ставший символом детства для нескольких поколений.
А ещё эта головоломка заложила золотое правило: чем проще и понятнее механика игры, тем выше шанс, что она завоюет рынок и разойдется, как горячие пирожки. Так оно и вышло. Актуально до сих пор.
В общем, об этой чудной игре и поговорим.
Теорема о четырех красках
2 мин
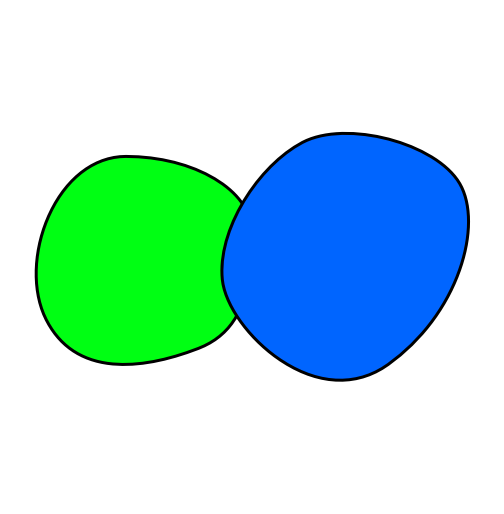
Натолкнулся в Интернете на задачу, которая называется "Теорема о четырех красках".
Вот ее страница в Википедии. Если не знаете эту задачу, то прочтите - интересная история.
Сама задача звучит так: сколько минимум нужно красок, чтобы раскрасить государства на карте, и при этом чтобы все граничащие территории имели разный цвет?
Многократные попытки решить эту задачу в течение последних ста лет интригуют, а итоговое ее решение исключительно благодаря компьютерам и некоему "специальному программному обеспечению" звучит как-то не очень убедительно. Поэтому попробуем разобраться самостоятельно.
Приступим.
Авторское право на сгенерированный лабиринт?
1 мин
Программист Джим Бамгарднер (Jim Bumgardner) в свободное время увлекается составлением лабиринтов. На днях он посетил супермаркет и увидел пачку с макаронами Kraft Mac & Cheese, на которой изображено «что-то очень знакомое».
Для постороннего человека картинка может показаться ничем не выдающейся, но Джим потратил много лет на написание программного обеспечения для генерации таких лабиринтов. Если посмотреть внимательнее, то можно увидеть вершины спирали Фибоначчи. По словам автора, это довольно уникальный дизайн.
Для постороннего человека картинка может показаться ничем не выдающейся, но Джим потратил много лет на написание программного обеспечения для генерации таких лабиринтов. Если посмотреть внимательнее, то можно увидеть вершины спирали Фибоначчи. По словам автора, это довольно уникальный дизайн.
Задачка для знатоков MySQL
1 мин
Добрый день, вот столкнулся с задачей, простой с виду, но для решения которой нужно хорошенько пошевелить мозгами :)
Итак: имеем следующую таблицу:
Нужно проставить место (place) в рейтинге каждой записи, базируясь на баллах (rating), причем, если баллы совпадают — использовать вторичный признак (в данном случае — id). В результате нужно получить следующую таблицу:
Важное замечание: ответом должен являться один запрос UPDATE (вложенные SELECT запросы использовать можно).
Жду предложений :)
Итак: имеем следующую таблицу:
| id | rating | place |
|---|---|---|
| 1 | 86 | NULL |
| 2 | 5 | NULL |
| 3 | 5 | NULL |
| 4 | 41 | NULL |
| 5 | 1 | NULL |
| 6 | 91 | NULL |
Нужно проставить место (place) в рейтинге каждой записи, базируясь на баллах (rating), причем, если баллы совпадают — использовать вторичный признак (в данном случае — id). В результате нужно получить следующую таблицу:
| id | rating | place |
|---|---|---|
| 1 | 86 | 5 |
| 2 | 5 | 2 |
| 3 | 5 | 3 |
| 4 | 41 | 4 |
| 5 | 1 | 1 |
| 6 | 91 | 6 |
Важное замечание: ответом должен являться один запрос UPDATE (вложенные SELECT запросы использовать можно).
Жду предложений :)
Игра о квадратах
1 мин
Со времён игры «2048» не было новых таких же увлекательных головоломок. Теперь есть: «Игра о квадратах».
НЛО Рубика (Rubik's UFO)
1 мин
Эта игрушка в Росcии появилась около года назад, но популярности так и не обрела.
Собрать НЛО значит сопоставить цветные сектора друг с другом. Все было бы просто, но у НЛО еще и 2 разных стороны — черная нижняя и серая верхняя, что существенно усложняет задачу.
Пятничный мини-CTF
1 мин
Приветствую всех хабрачитателей. Я очень люблю поразмять свои мозги разными задачками — это могут быть какие-то математические задачи, интересные головоломки, связанные с программированием, или какие-то ctf-таски.
Для тех, кто хочет разнообразить пятницу головоломками я хочу предложить свой мини-ctf, в котором всего три задачки.
XT_CTF_01
XT_TASK_101
Ссылка на таск: xt_task_101.zip
Формат флага: XTGFLAG{…}
SHA1 флага: 6980D76C3C5246A101820A77031CA0EBE84A4A0E
XT_TASK_102
Ссылка на таск: xt_task_102.zip
Формат флага: XT{…}
SHA1 флага: 16448BF22750DE7E575A5A86E739FA9018ACFE52
XT_QUEST_103
Ссылка на таск: xt_quest_103.zip
Количество уровней: 15 + бонус
Для тех, кто хочет разнообразить пятницу головоломками я хочу предложить свой мини-ctf, в котором всего три задачки.
XT_CTF_01
XT_TASK_101
Ссылка на таск: xt_task_101.zip
Формат флага: XTGFLAG{…}
SHA1 флага: 6980D76C3C5246A101820A77031CA0EBE84A4A0E
XT_TASK_102
Ссылка на таск: xt_task_102.zip
Формат флага: XT{…}
SHA1 флага: 16448BF22750DE7E575A5A86E739FA9018ACFE52
XT_QUEST_103
Ссылка на таск: xt_quest_103.zip
Количество уровней: 15 + бонус
Разборы задач мини-CTF
7 мин
Приветствую всех хабрачитателей. Прошло три недели с момента, как я предложил желающим порешать мой CTF и, думаю, что пора опубликовать разборы задач. По своему опыту знаю, что очень обидно быть в ситуации, когда потратил кучу времени на задачу, а решения так и не узнал, поэтому выкладываю разбор задач. Решения разбиты на шаги и скрыты под спойлер, чтобы после любого шага можно было попробовать дорешать задачу самому, преодолев сложный момент.