Пользователи решили выяснить, почему при запросе «Turn! Turn! Turn!» в Google на первом месте появляется внутренний калькулятор поисковика, отображающий значение «241217.524881». Видео на YouTube, где The Byrds исполняют одноименную песню Пита Сигера, появляется при этом лишь на второй строчке.
Как полюбить математику и подружиться с ней на всю жизнь, если ты уже не школьник

«Вспоминаю, как в 7-м классе ничего не понимал, когда мы начинали разбирать тригонометрию. С учителем мы не смогли найти общий язык, поэтому к 8–9-му классу я был уверен, что никогда не буду заниматься математикой, а уж тем более сидеть по несколько часов в день, утыкаясь в учебники Беклемишева или Кожевникова и параллельно просматривая лекции Физтеха…»
Всем привет! Идею этой статьи я вынашивал довольно долго, пока не набрался опыта в том, что сейчас стало моей каждодневной практикой. Надеюсь, мой опыт поможет кому-то из вас комфортнее и эффективнее подойти к изучению математики (а может, и других наук). Предлагаю познакомиться:
Меня зовут Ренат, мне 23 года, я родился в Москве, окончил обычную школу и вплоть до 19 лет не понимал, чем хочу заниматься — что называется «что меня драйвит». Сейчас живу на Кипре, работаю тут аналитиком, продолжаю параллельно учиться в России и скоро заканчиваю там университет.
За последние несколько лет я успел поработать аналитиком в Ozon, затем продуктовым аналитиком в Тинькофф (ныне Т-банк), перешёл в лондонский стартап, а сейчас тружусь над проектами в сфере Trust & Safety. И вот в один прекрасный день я решился «серьёзно ботать математику»: уже несколько месяцев уделяю 10–15 часов в неделю задачам, лекциям и подготовке к поступлению в магистратуру (решая вступительные от МГУ, ВШЭ, МФТИ). Именно об этом пути — как я ищу мотивацию, борюсь с прокрастинацией и стараюсь не выгореть — я и хочу вам рассказать.
Парадокс Гранди. Как современные школьники повторяют ошибку Лейбница и Эйлера

Было у отца два сына. И оставил он им наследство — камень драгоценный. А чтобы никого не обидеть, поставил он перед сыновьями условие: нельзя тот камень ни пилить, ни продавать. Можно только по очереди владеть им. И повелось так — каждый год камень переходил от одного брата к другому. Потом камнем по очереди владели их потомки, потом потомки их потомков… И длилось так вечно.
Этой притчей итальянский математик, монах и философ Гвидо Гранди пытался объяснить решение задачи, которую сам же и сформулировал. В 18 веке её считали парадоксом и предлагали разные варианты решения. Долгое время она не давала покоя математикам.
Задача Гранди формулируется очень просто: какой результат мы получим, если будем до бесконечности складывать 1 и -1?
Что такое мат.анализ и с чем его едят?
Давайте знакомиться: я Меликян Маргарита, кандидат физико-математических наук, уже 4й год работаю на мехмате МГУ и кафедре высшей математики МФТИ, а также несколько лет как преподаю в ШАД Helper. Преподаю я как разнообразные курсы из блока анализа, так и вероятностного блока, и сегодня я хочу немного поговорить о том, каково это – осваивать математический анализ и каких ошибок следует избегать, какие лайфхаки применить.
Первая препона, с которой сталкивается человек в самом начале освоения новой дисциплины, даже если он это делает “под присмотром” преподавателя – это литература. На что нужно обращать внимание и ориентироваться при выборе?
Формула, соединяющая е и пи

Факториал натурального числа определяется так:
. Например,
- число со 157 цифрами. Формула, о которой пойдёт речь далее, используется для оценки факториала при больших
.
Конспект по «Машинному обучению». Математический анализ. Градиентный спуск
Вспомним математический анализ
Непрерывность функции и производная
Пусть
Определение 1 (предел функции по Коши):
Функция
Обозначение:
Интуитивное объяснение интеграла. Часть I — от умножения натуральных чисел до Ньютона и Лейбница

Если у Вас нет математического образования, если Вы хотите по-настоящему разобраться в том, что из себя представляет интеграл и интегрирование, зачем всё это надо, как математика пришла к идее интеграла, то в таком случае Вы пришли по адресу — добро пожаловать!
Греки, черепаха и матанализ

Касательно этого поста меня терзали сомнения. С одной стороны, история вроде как широко известная. С другой, я не раз сталкивался с тем, что общеизвестное для одних оказывается новой информацией для других (это и ко мне относится). Так что, кто в курсе, не ругайтесь, опять же школьникам может пригодиться.
Физтех запускает онлайн-курсы по высшей математике для подготовки к поступлению в магистратуру

Онлайн-курсы МФТИ по высшей математике предназначены для самостоятельной теоретической и практической подготовки к поступлению в магистратуру Физтеха и других ведущих технических университетов.
- Уже открыто обучение по курсам «Математический анализ — 1», «Аналитическая геометрия и линейная алгебра»;
- 1 декабря станут доступны курсы «Математический анализ — 2», «Дифференциальные уравнения» и «Теория вероятностей»;
- 31 декабря откроются курсы «Теория функций комплексного переменного» и «Уравнения математической физики».
Математика для Data Scientist: необходимые разделы
Для специалиста Data Science важны следующие направления математики:
- статистика;
- теория вероятностей;
- математический анализ;
- линейная алгебра.
В предыдущей статье «Data Science: книги для начального уровня» специалисты Plarium Krasnodar рекомендовали литературу по программированию на Python, а также по визуализации результатов и machine learning. В этой статье они предлагают подборку материалов и книг по математике, полезных в Data Science.

Прекрасные чудовища математики

UPD: добавлен график функции.
Подобно своему создателю Карлу Вейерштрассу, это чудовище возникло из ниоткуда. Потратив четыре года учёбы в университете на кутежи и фехтование, Вейерштрасс выпустился из него с пустыми руками. В конце концов он взялся за преподавание и бо́льшую часть 1850-х был школьным учителем в Браунсберге. Ему была отвратительна жизнь в маленьком прусском городишке, он находил своё существование там одиноким. Единственной отдушиной для него стали математические задачи, над которыми он работал между уроками. Но ему не с кем было поговорить о математике, и у него не было технической библиотеки для обучения. Даже результатам его работ не удавалось покинуть пределов Браунберга. Вместо публикации в академических журналах, как это сделал бы университетский исследователь, Вейерштрасс добавлял их к школьным проспектам, пугая потенциальных учеников заумными уравнениями.
В конце концов Вейерштрасс отправил одну из своих статей в уважаемый «Журнал Крелле». Несмотря на то, что предыдущие статьи остались едва замеченными, эта вызвала огромный всплеск интереса. Вейерштрасс обнаружил способ работы с ужасным классом уравнений, известным как «абелевы функции». В статье было приведено краткое изложение его методов, но этого было достаточно, чтобы убедить математиков в наличии у автора уникального таланта. Не прошло и года, как Кёнигсбергский университет дал Вейерштрассу почётную докторскую степень, а вскоре после этого Берлинский университет предложил ему должность профессора. Несмотря на то, что Вейерштрасс проделал интеллектуальный аналог пути «из грязи в князи», многие из его старых привычек сохранились. Он редко публиковал статьи, предпочитая делиться своими работами со студентами. Но он был малопочтителен не только к процессу публикации: не пугали его и «священные коровы» математики.
Мир математики глазами AI

Всем привет! В этой статья я хочу посмотреть, как AI видит мир математики, а точнее, какие разделы знает, насколько понимает, про что они и какие основные результаты может выделить.
Для этого я буду использовать популярный сейчас ChatGPT, который как-то так предложил мне начать эту статью.
Пишем графический ASCII-калькулятор с помощью стандартной библиотеки Си
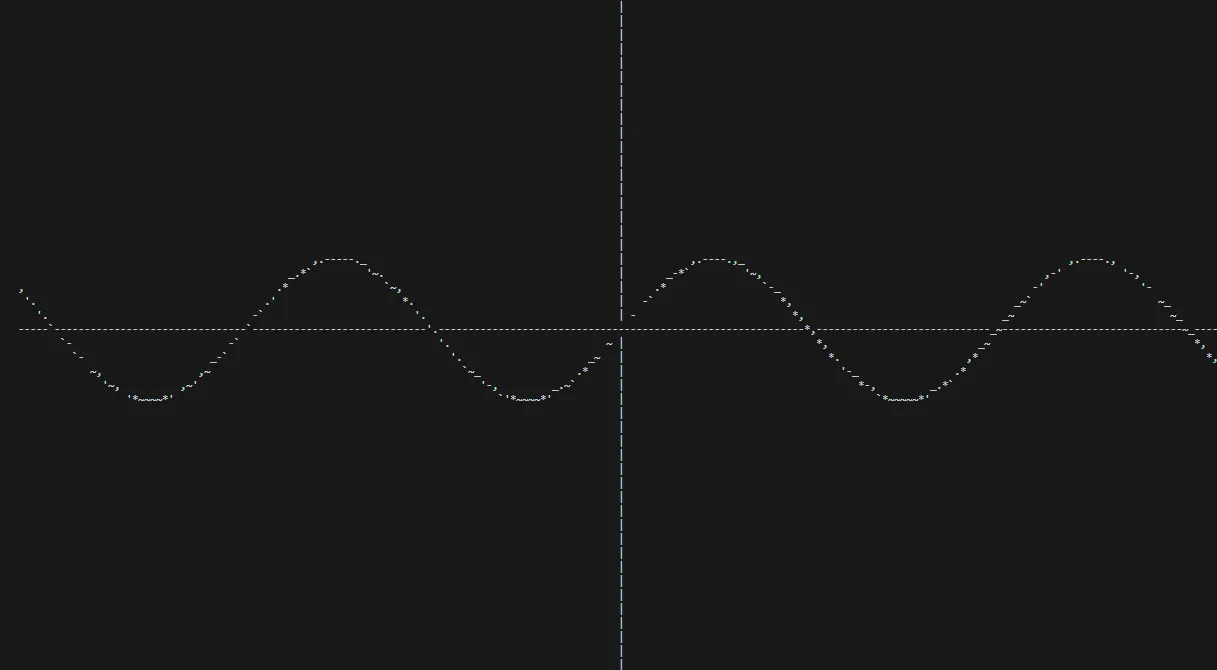
Программа calculator.c родилась как школьный проект в рамках Student Innovation Scholarship. Сперва я решил написать простой инструмент для построения графиков функций с помощью символов ASCII, но после завершения первого прототипа понял, что задача намного сложнее, чем предполагалось. Вернувшись к проекту год спустя, я увидел, что в нём есть много неочевидных нюансов. Поэтому предлагаю разобрать весь процесс разработки моего графического калькулятора с нуля.

История науки: как математический анализ развился из древних парадоксальных загадок и религиозных споров Средневековья

Сегодня, живя в 21 веке, в постиндустриальном обществе мы привыкли довольно жестко противопоставлять науку и научное мировоззрение всем остальным способам познания мира и описания реальности. Однако, как указывал еще философ 20 века Пол Фейерабенд, в реальности на больших отрезках истории всё выглядело совсем иначе: наука, религия, умозрительные размышления и даже эзотерические фантазии порой шли рука об руку, помогая, идейно обогащая и стимулируя друг друга.
Почему апории Зенона на самом деле не решены до сих пор и как это связано с фундаментальными вопросами современной науки

Это будет очень большая статья, в рамках которой я бы хотел обсудить одну проблему, которая подавляющему большинству людей кажется абсолютно незначительной и уже давно решенной, однако на самом деле это проблема не решена и она не просто не незначительна, но имеет огромное фундаментальное значение в контексте развития современного естествознания. Речь идет об апориях Зенона. Если ранее вы о них ничего не слышали или слышали только мельком, то приготовьтесь, сейчас вам откроется целый удивительный мир, в котором сходятся в одно целое математика, философия и естествознание. Если об апориях вы хорошо осведомлены и считаете, что я решил вновь попереливать из пустого в порожнее давно решенные в математическом анализе древние загадки, то будьте готовы расстаться с прежними шаблонами и взглянуть на мир совершенно под другим, весьма неожиданным углом. Статья будет сложной, но я хочу, чтобы она оказалась понятной и новичкам и людям опытным в разных науках, поэтому она будет объемной, так как придется многие моменты подробно разъяснять. Моя цель - показать, что мир совсем не такой, каким кажется. Показать, что древние логические парадоксы - это нечто гораздо большее, чем просто веселые задачки для ума. Показать, что философия - это не просто словоблудие, а истинный способ заглянуть за ширму мироздания, но только при условии, что философ готов опираться на математику и физику, а физики и математики готовы мыслить по-настоящему философски (как эти делали, кстати, абсолютно все величайшие ученые в истории человечества).
Гробы на экзаменах в ШАД
Автор: Лыков А., к.ф.-м.н., академический руководитель Школы Высшей Математики и ШАДХелпера.
Гробом принято называть задачу на экзамене или олимпиаде, которую почти невозможно решить.В статье мы приведём несколько примеров из вступительных экзаменов в ШАД и классифицируем гробы на три типа.
В контексте экзаменов в ШАД, гробы появляются на экзаменах не каждый год и, как правило, находятся среди последних задач письменного экзамена. Выделим следующие типы гробов.
I) ''Классический'' — решение у задачи существует, полностью опирается на программу, использует необычные приёмы в решении, сложная даже для специалистов. Примеры:
Рваная, чудовищная функция, которая сломала математический анализ

На просторах англоязычного Интернета нашел еще одну вдохновляющую (лично меня по-крайней мере) статью. Машинный перевод, как всегда, оставляет желать лучшего, так что, как всегда, делюсь со всеми интересующимися своим авторским переводом. Оригинал здесь. Приятного чтения!
В конце XIX века Карл Вейерштрасс изобрел фрактальноподобную функцию, которая была осуждена математическим научным сообществом как "безобразное зло". Со временем она преобразила основы математики.
Постигаем интегралы с помощью Maple
Иллюстрируя вышесказанное, в этом посте я расскажу о нескольких различных сценариях использования СКА Maple в борьбе с интегралами. Надеюсь, что персоны, знакомые с тонкостями символьных вычислений, найдут для себя здесь что-нибудь новенькое. А для тех, кому такой способ решения задач в новинку, я постаралась добавить побольше комментариев.

Mathcad Express — бесплатный математический редактор, про который мало кто знает
РТС Mathcad – это характерный пример математического ПО, предназначенного для осуществления, как численных, так и аналитических расчетов по формулам и визуализации их результатов в виде графиков.
Задача о конфетах (улучшаем результат)
Необходимо было найти максимально допустимое отклонение массы конфеты при ее производстве, чтобы нетто коробки, состоящей из 12 штук их, не выходило за пределы 310±7 грамм в 90% случаев. Закон распределения считать нормальным.
Был получен ответ, что если среднеквадратичное отклонение
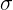 массы конфеты при производстве не превышает
массы конфеты при производстве не превышает 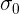 =1,2248, то данная величина не ограничена сверху.
=1,2248, то данная величина не ограничена сверху.Под катом вас ожидает улучшение полученного результата по модулю некоторых, как мне кажется — разумных, предположений. Дальнейшее изложено недостаточно строго, но всё же требует знаний математического анализа и теории вероятности в объёме технического вуза.